Аннотация

A number of sectors in the food industry practice cooling substances of biological origin. This contributes to the maintenance of their biological properties, as well as prevents microflora growth in the product. One of the ways to intensify production processes and maintain the quality of raw materials and finished products is their accelerated cooling with the help of low-energy cooling equipment. The use of physical bodies cooled to low temperatures is a promising way to accelerate liquid cooling. We used balls with frozen eutectic solution. In our research, the problem of cooling a liquid system is formulated and solved within the framework of classical linear boundary value problem for the equation of a stationary convective heat transfer. In the area of the actual values of the process parameters on the study object, the solution obtained is used as the basis for numerical experiment on the modelling of the cooling liquid flow with the cooling agent system, namely balls filled with eutectic solution. By calculation, the efficiency of the proposed method for cooling liquid was justified based on such factors as temperature, the number of balls in a two-phase liquid system, and the duration of low-temperature treatment. The presented results of the numerical experiment complied with real heat transfer processes during liquid cooling.

Ключевые слова

Low-temperature treatment, cooling, liquid system, heat transfer, eutectic solution

ВВЕДЕНИЕ

An important issue of the intensification of production processes and rational use of raw materials is the possible rapid decrease in the temperature of the liquid system. For example, in processing industries and other sectors of the economy, the cooling of biological origin substances contributes to the maintenance of their biological properties, as well as prevents microflora growth in the product [1, 2].

Currently, the cooling of liquids by using frozen solids is one of the methods for lowering the temperature in a liquid medium [3–7, 11, 14, 15]. This technology is useful and in refrigeration engineering, where frozen physical bodies are balls filled with eutectic solution [8–10, 12]. This is confirmed by results of theoretical and experimental studies conducted by reserchers of Moscow State University of Food Production and Razumovsky Moscow State University of technology and management. The results confirm the advantages of cooling water with frozen balls over other methods, providing a high intensity of the process and reduced energy consumption.

To accelerate the heat transfer process based on water treatment using the technology of enrichment of the working volume of cooling liquid with frozen bodies (cooling agent), it is advisable to carry out this process in the mode of flow of the liquid through a container with frozen balls. At the same time, it should be noted that there are no theoretically based calculation methods for predicting and controlling the heat transfer process, including in the flow, when the cooling process develops in a heterogeneous liquid “water-frozen balls” system.

Bases on the law of conservation of mass and energy, we presented the results of the analytical and numerical studies on the of cooling a liquid flow moving through a heat exchanger filled with balls with a frozen eutectic coolant to justify the intensification of the heat transfer process between a coolant and liquid.

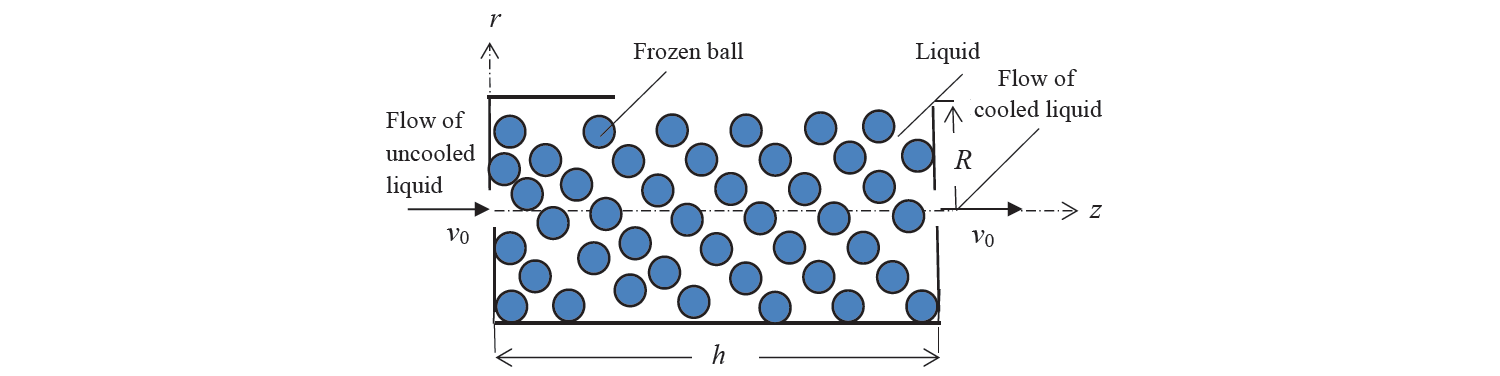
The setting of the problem. Let a liquid flow (for example, water) be supplied to a certain container filled with balls with frozen eutectic solution in a stationary mode, with a small productivity Q and a low flow rate v₀ (Fig. 1). We will consider the selected motion model of a two-phase liquid system as the filtration flow of a fluid through a porous medium formed by balls (coolant) [6].

It is assumed that the balls are statistically uniformly distributed inside a cylinder of length h and radius R containing a liquid (water) and solid (balls) phases.

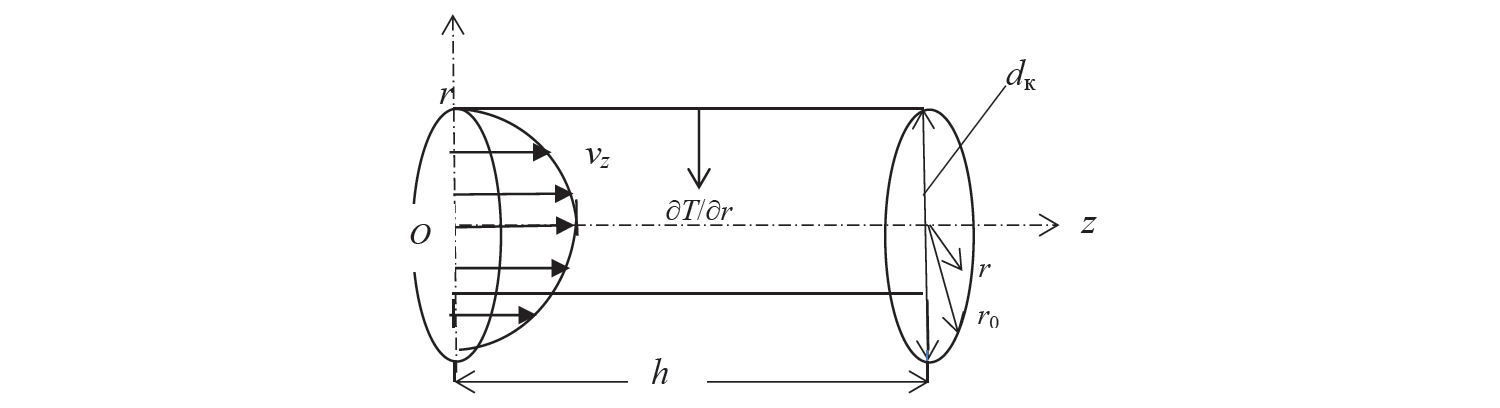
To simplify the process for quantitative analysis of the heat removal from the liquid to the balls, we replaced the pore volume occupied by the liquid (preserving the values of porosity) with a set of cylindrical tubes (conditionally, capillaries). Each of them had an axis parallel to the axis of the vessel, length h and reduced radius r₀ (Fig. 2).

For the selected geometric model of the liquid volume, we introduce the following notations: d_b is the ball diameter and m is the surface porosity of the system (m < 1), numerically equal to the ratio of the volume of liquid filled pores to the volume of the system [8].

Since the volume and surface porosities of the working volume of the capacitance are quantitatively the same [8], the approximate ratio, based on the porosity definition can be written as follows:

which yields the relationship:

henceforward, r₀ = r₀ (d,m), d = d_b is the diameter of the ball.

Thus, as can be seen, the problem of calculation reduces to the quantitative analysis of temperature in the isolated capillary.

The solution of the problem. Due to the possible axisymmetric nature of heat transfer from the walls of the channel to the liquid, the quantitative modeling of this process will be carried out in a cylindrical coordinate system, in the meridional section of the channel rOz (Fig. 2).

For the selected simulation geometric model, we use the equation of stationary convective thermal conductivity related to cylindrical coordinates as a basic differential equation describing the heat transfer phenomenon in the flow [9]:

where r, z – radial and axial coordinate, respectively; T – the temperature of water; v_z – axial component of fluid flow rate in the capillary; а = λ/(сρ), а – is the coefficient of thermal diffusivity of water, λ – thermal conductivity coefficient, c – specific conductivity coefficient, and ρ – is the density of water.

In practice, fluid rate v_z can be replaced with its averaged value over the cross section of the channel, with a small error. Then a simplified form of Eq. (2) can be written as follows:

where

v_z = v₀/m, v₀ = Q/S – volume rate of fluid flow in the capacitance (filtration rate [8]), S = πR₂ – cross-sectional area of the capacitance; β is the specific coefficient of thermal diffusivity calculated taking into consideration axial velocity v_z.

For simplicity, assume inlet temperature to be constant:

The condition of symmetry of the temperature distribution along the channel diameter corresponds to the condition of the maximum temperature in the middle the capillary walls.

Taking into account the fact that heat energy develops from the liquid to the capillary wall, the boundary condition on the surface of this channel is:

where Н = α /λ, α is heat transfer coefficient from the liquid to the capillary wall, Т_k is the eutectic temperature of frozen balls (Fig. 1).

According to (5)–(7), in the framework of the terminology adopted in the theory of heat transfer, we have a problem with boundary conditions of the third kind for differential equation (3).

From the point of view of quantitative analysis of the thermal regime in a steady stream of fluid inside the capillary, the considered problem is formally equivalent (provided that the diameter of the capillary d_k is much less than the capacitance height h) to the problem of the temperature distribution over time in an unsteady mode in an unlimited cylinder. What is more, in Eqs. (3)–(7) the duration of the heat transfer process is displayed on the axial coordinate z.

Thus, the solution to the problem with an unsteady mode of heat transfer in an unbounded cylinder can be adapted to the boundary value problem (3)–(7) of the temperature distribution in the convective fluid stream in the capillary and is formulated as a dependence:

where

is specific value reflecting the differential temperature of the ball Т_k and the initial temperature of the liquid Т₀, as well as the current differential temperature of the liquid Т(d,m,r,z) and the coolant temperature Т₀.

where J₀, J₁ – Bessel function of the first kind of zero and first order respectively; positive roots of transcendental equations.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Quantitative modeling of the heat transfer process was carried out based on relations (8)–(13) using the Mathcad medium.

We used the following process parameters: the length of the capacitance h = 0.5 m; the diameter of the capacitance D = 0.1 m; equipment productivity (by water) Q = 2×10^–4 m³/s; kinematic viscosity coefficient ν = 10^–6 m²/s; ball eutectic temperature Т_k = – 10°С; thermal c onductivity c oefficient λ = 0.58 W /(m·К); thermal diffusivity coefficient a = 13.8×10^–8 m²/s; and ball diameters d = 0.0375, 0.04, and 0.0425 m. The calculation of the current temperature of the liquid was carried out according to two variants of porosity: m = 0.5 and m = 0.35.

In accordance with the selected parameter values, the volume rate of flow (filtration rate) for all calculation options was v₀ = 4Q/(πD²) = 4×2×10^–4/(3.14×0.1²) = 0.0254 m/s.

As a calculated value of the temperature θ given over the radius r inside the capillary, we used its value θ_av, averaged over the channel cross-sectional area:

The following dependence was used as a calculated dependence for the liquid temperature based on the operating parameters of the axis coordinate z and the time of the process τ:

To calculate the number of balls N in the capacitance, we used the formula:

where m is the porosity if the liquid system, d is the diameter of the ball, D is the diameter of the capacitance, and h is the length of the capacitance.

Thus, according to the geometrical parameters, the number of balls of diameter d = 0.04 m was 58 for m = 0.5 and 76 for m = 0.35.

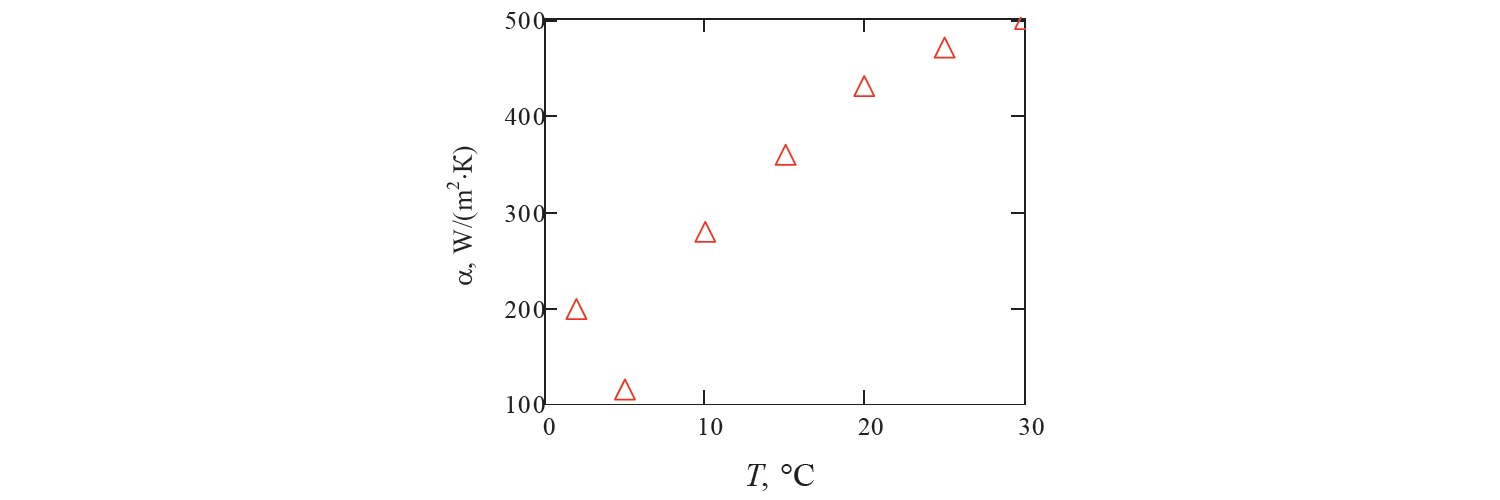
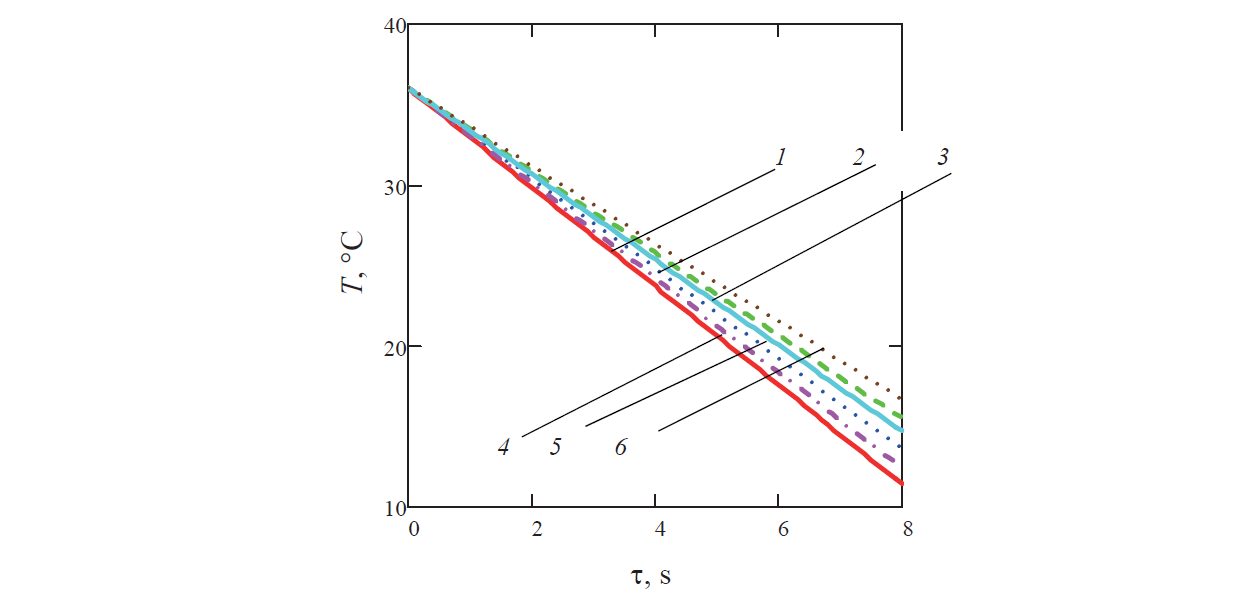
Previously, to assess the convergence of series (8), we performed test calculations using formula (14). Temperature T₀ was 36°С and heat transfer coefficient α was 440 W/(m²·К) ( Fig. 3 ). B ased on Bi = αr₀/λ = 440×0.02/0.58 ≈ 15, we found partial sums of this series, from the first to the sixth sum inclusively.

Since determination of the roots of transcendental equation (11) when varying the parameters of the Bi criterion involves laborious calculations, we used tabular data. As in all calculations a slight difference in the value of partial sums was noted only starting from the sixth sum (Fig. 4), the sum of six members of this series was used in the calculations (8).

In addition, to find the dependence of temperatures in the capillary on the diameter of the balls for each of the options, we considered the situation when balls with a diameter of 0.0375 or 0.0425 m (closed to the diameter of the test ball d = 0.04 m) acted as a coolant. This made it possible, with some approximation, to use tabular data [13] on the roots of equation (11) based on Bi = αr₀/λ = 15 which corresponded to d = 0.04 m.

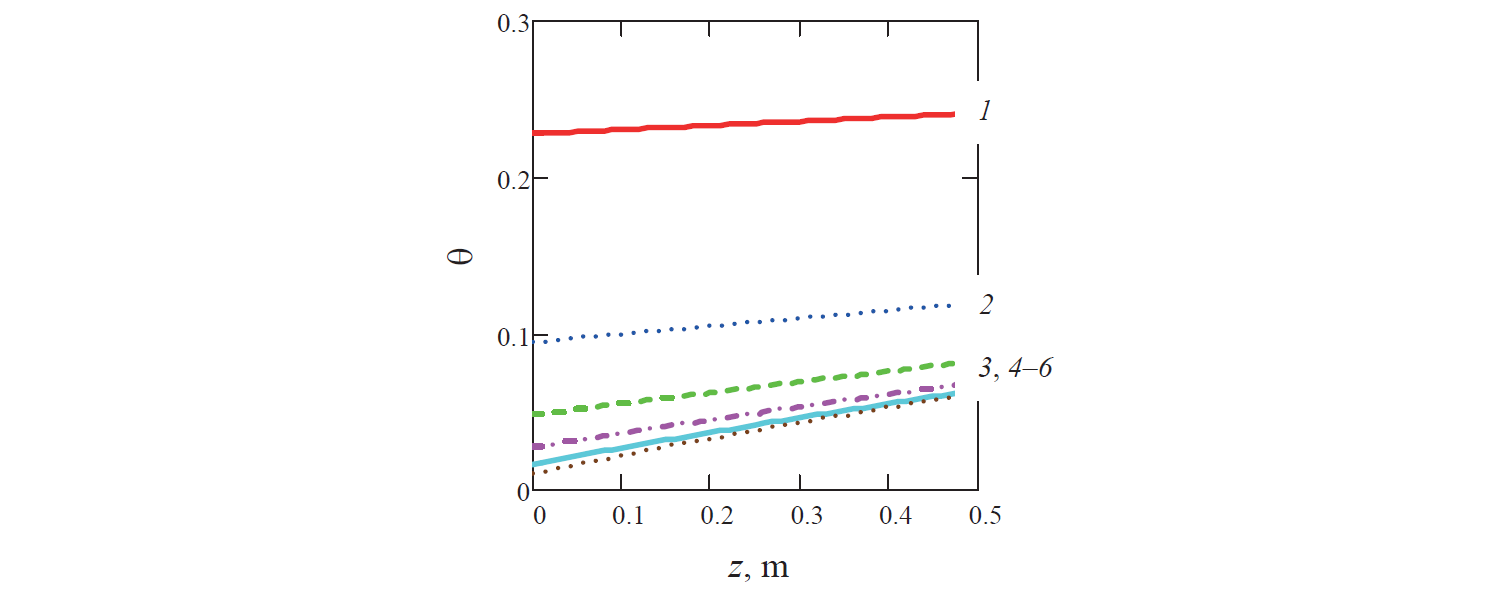
From relations (8)–(13) and (15), in the range of variation of the parameters of water cooled by frozen balls, 7 calculation results were obtained and graphs were plotted (Figs. 5–7). Based on the analysis of the graphs, the dependence of the variables of the considered problem on the operating parameters was revealed.

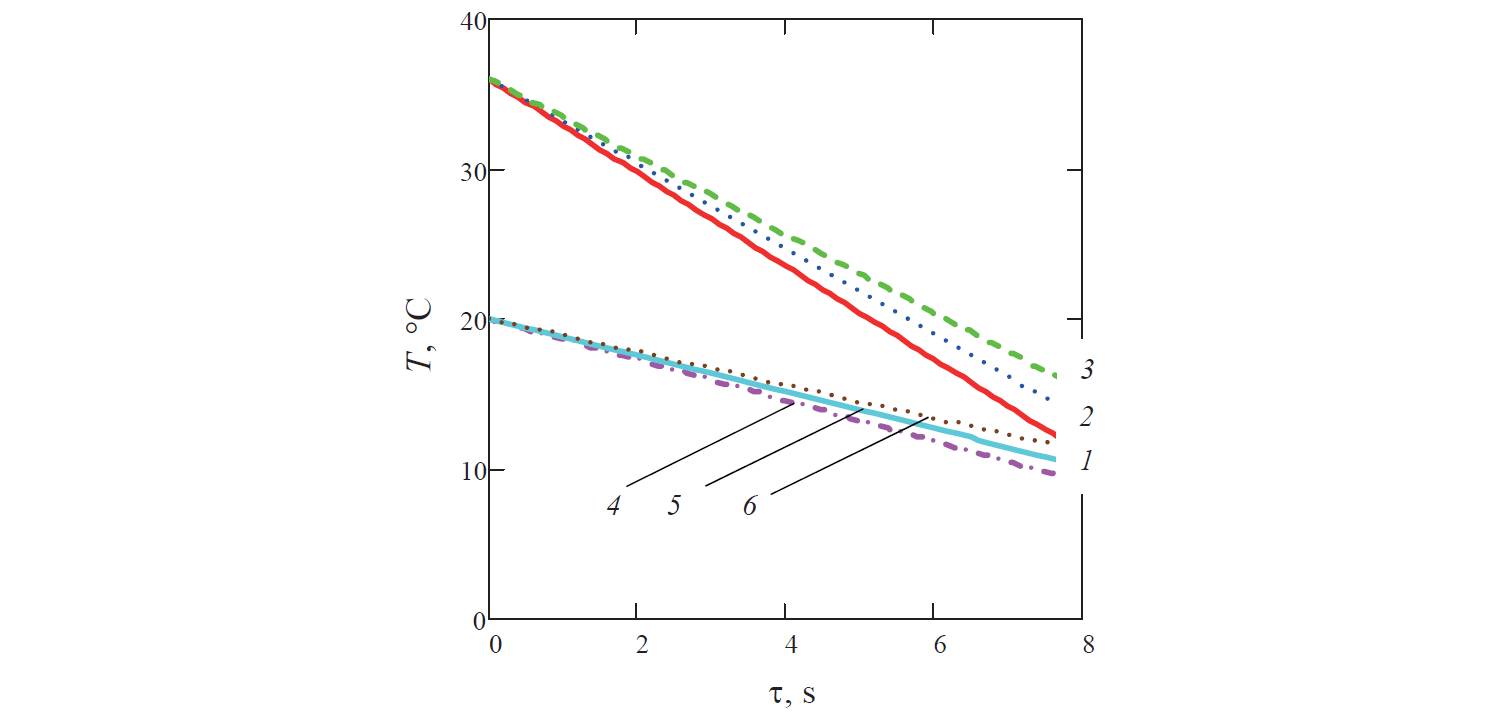
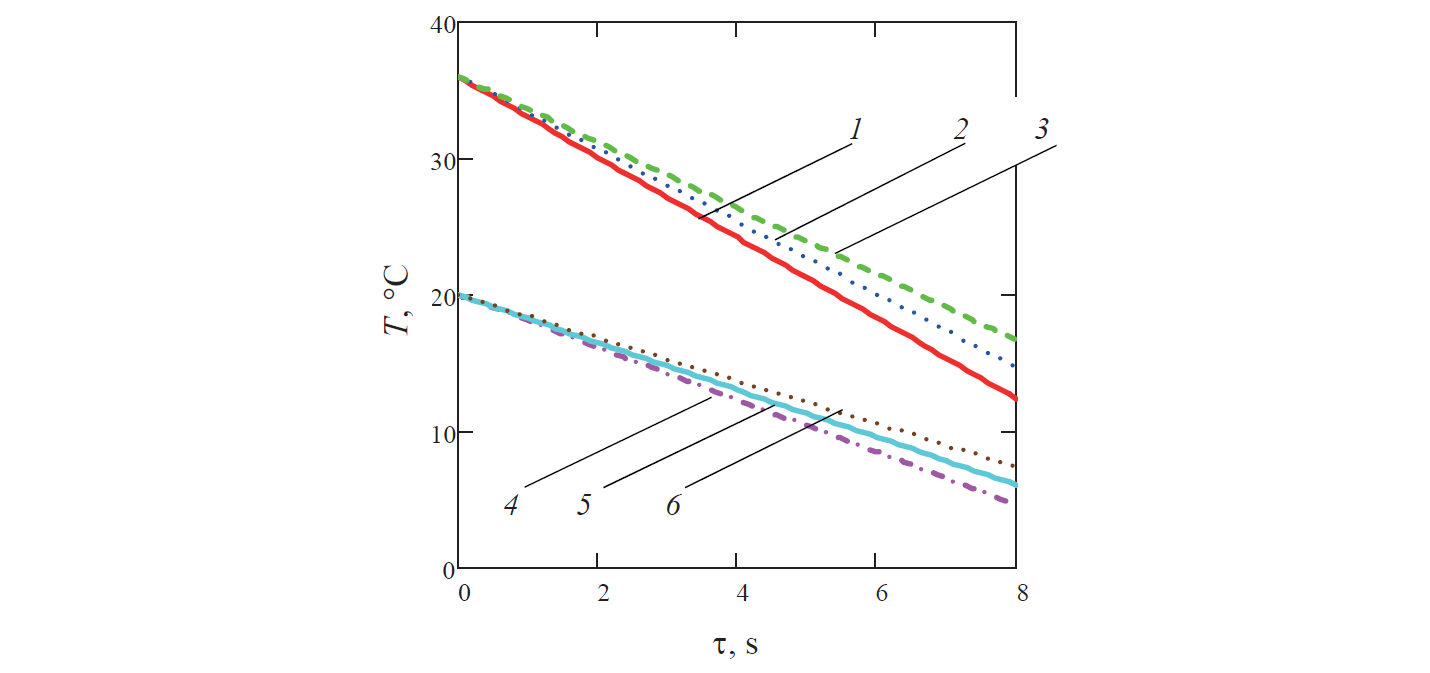
Since the calculated temperature of the coolant reduced along the channel (Fig. 4), the specific temperature of the liquid θ increased in the same direction.

In turn, the rate of change in the temperature of the liquid decreased with time (Figs. 5–7). This is because of the reduction of the specific surface area of the ball, which is the ratio of the surface area of the ball to its volume. This resulted in decreasing heat exchange on the border between solid and liquid phases in the liquid system (for example, in Fig. 5 graph 3 corresponding to the diameter of the ball d = 0.0425 m is above graph 2 for the ball diameter d = 0.04 m).

In addition, as it can be seen from Fig. 7, in the case of water productivity Q fixed for all variants, the increase in the rate of flow of the coolant along with the decrease in the porosity of the liquid system naturally leads to a decrease in the rate of cooling of the liquid. Thus, for example, in Fig. 7 graph 4 corresponding to porosity m = 0.35 and the diameter of the ball d = 0.04 m is above graph 1 for porosity m = 0.35 and the ball with the same diameter.

However, it should be noted that, despite the qualitative consistency of the calculated results with the physical meaning of the process under study, the quantitative assessment that characterizes the course of this process needs additional comments.

First of all, this relates to the question of formalizing the boundary condition at the interface, which is typical for many works on the theory of heat conductivity, where, when setting the problem, the temperature is assumed unchanged, while for the heat exchange between phases (for example, between liquid and coolant) phase temperature tends to level off. This leads to a decrease in the intensity of heat transfer from the liquid to the ball as naturally as in the studied problem.

Therefore, the results of the the cooling rate of water presented in Figs. 5–7 on, in fact, are overestimated compared to real data.

At the same time, despite the simplifications based on the theory of heat conduction and used in the formulation of the problem, physical and mathematical modeling of processes makes it possible to predict and control their development. To the same extent, this is also applied to the complex problem of justifying the rate of liquid cooling due to the accumulation of frozen balls with a developed heat exchange surface that is analyzed in this paper.

ВЫВОДЫ

To justify heat transfer from the fluid flow to balls with eutectic frozen solution, we applied an analytical tool forecasting the course of this process in the innovative technology for cooling this liquid.

In the quantitative analysis of this problem kinetic aspects of filtration fluid motion was used, namely, when the working volume occupied by the liquid between the balls was simulated by equivalent plurality of ordered cylindrical capillary channels. This allowed us, from the point of view of analytical and numerical analysis of the thermal regime in a steady fluid flow inside the working volume of the capacitance, to adapt the solution of this problem to the study of this regime in an isolated capillary.

The accepted conditions, namely the size of the capacitance and balls and the volume fraction of balls in the capacitance created the preconditions for conducting quantitative modeling of the process under study based on the calculated dependences of the temperature distribution in an unlimited cylinder under an unsteady regime.

To assess the efficiency of the cooling process of fluid flow in a heat exchanger with a frozen solid phase and a developed heat exchange surface in the field of the real values of the process parameters, the obtained temperature dependences were used to carry out a numerical modeling of the cooling process of this medium.

Based on the results of the analytical and numerical study of the problem, an acceptable region for varying the mechanical and thermotechnical parameters of these processes was determined. This region is of importance for engineering calculations of the low-temperature processing of raw materials and finished products of biological origin.

КОНФЛИКТ ИНТЕРЕСОВ

The authors declare that there is no conflict of interest related to the publication of this article.

СПИСОК ЛИТЕРАТУРЫ

1. Panin AA, Kozlovtsev AP, Kvashennikov VI, Korovin GS. Energy-saving method of dairy produce cooling. Izvestia Orenburg State Agrarian University. 2013;41(3):97–99. (In Russ.).
2. Kvashennikov VI, Kozlovtsev AP, Shakhov VA, Kryuchin NP. Energy-saving technology of storing natural ice at dairy farms. Scientific Review. 2015;(4):17–21. (In Russ.).
3. Ibrahim MT, Zacharias J, Briesen H, Först P. Heat transfer to a stationary cubic particle in a laminar tube flow: Computational fluid dynamics simulations and experiments. Journal of Food Engineering. 2020;274. DOI: https://doi.org/10.1016/j.jfoodeng.2019.109833.
4. Marazani T, Madyira DM, Akinlabi ET. Investigation of the parameters governing the performance of jet impingement quick food freezing and cooling systems – A review. Procedia Manufacturing. 2017;8:754–760. DOI: https://doi.org/10.1016/j.promfg.2017.02.097.
5. Vinogradov VV, Tyazhelʹnikova IL, Vinogradova EP, Esenbekov VS. Teoreticheskiy analiz vozmozhnosti upravleniya usloviyami zatverdevaniya v nepreryvnolitom slitke [Theoretical analysis of the possibility of controlling the solidification conditions in a continuously cast ingot]. Metally. 2014;(4):17–22. (In Russ.).
6. Vinogradov VV, Shakurov AG, Tyazhel’nikova IL, Vinogradova EP, Esenbekov VS. Mathematical simulation of melted slag cooling by a system of metal balls. Technical Physics. 2015;85(12):21–25. (In Russ.).
7. Yagov VV, Zabirov AR, Kanin PK. Heat transfer at cooling high-temperature bodies in subcooled liquids. International Journal of Heat and Mass Transfer. 2018;126:823–830. DOI: https://doi.org/10.1016/j.ijheatmasstransfer.2018.05.018.
8. Babakin BS, Voronin MI, Semenov EV, Belozerov GA, Babakin SB. Quantitative analysis of the process of cooling a coolant using developed frozen surfaces. Chemical and Petroleum Engineering. 2018;54(3–4):233–238. DOI: https://doi.org/10.1007/s10556-018-0468-1.
9. Babakin BS, Semenov EV, Voronin MI, Slavyansky AA, Babakin SB, Suchkov AN. Calculation of the process of preparation of the chilled water frozen balls. Storage and Processing of Farm Products. 2016;(8):15–19. (In Russ.).
10. Semenov EV, Babakin BS, Voronin MI, Belozerov AG, Babakin SB. Mathematical modeling of thermostating liquid cooling process by the system of frozen ballons. Journal of International Academy of Refrigeration. 2016;(4):74–79. (In Russ.). DOI: https://doi.org/10.21047/1606-4313-2016-15-4-74-79.
11. Palacz M, Adamczyk W, Piechnik E, Stebel M, Smolka J. Experimental investigation of the fluid flow inside a hydrofluidisation freezing chamber. International Journal of Refrigeration. 2019;107:52–62. DOI: https://doi.org/10.1016/j.ijrefrig.2019.08.009.
12. Babakin BS, Voronin MI, Semenov EV, Babakin SB, Belozerov AG, Suchkov AN. Substantiation of liquid cooling by introducing the frozen balls with developed surface. Journal of International Academy of Refrigeration. 2019;(2):95–101. (In Russ.). DOI: https://doi.org/10.17586/1606-4313-2019-18-2-95-101.
13. Lykov AV. Teoriya teploprovodnosti [Theory of thermal conductivity]. Moscow: Vysshaya shkola; 1967. 599 p. (In Russ.).
14. Asgharian H, Baniasadi E. Experimental and numerical analyses of a cooling energy storage system using spherical capsules. Applied Thermal Engineering. 2019;149:909–923.
15. Levashov VYu, Puzina YuYu. The parameters influencing sphere cooling in a cold liquid. Journal of Physics: Conference Series. 2018;1128(1). DOI: https://doi.org/10.1088/1742-6596/1128/1/012041.