Аннотация

At this point in history, mankind faces a daunting challenge: how are we to produce high-grade foods without damage to the environment? The only possible rational solution lies in the efficient use of natural raw materials. However, the practical side of the matter cannot be resolved without innovative food equipment designed on the basis of the latest scientific achievements. The current research features the theory and practice of curd whey and skimmed milk ultrafiltration. It focuses on the main operating parameters of the equipment involved and the maximum permissible value of the milk solids content. The experiment included whey, obtained as a byproduct of cottage cheese processing, and skimmed milk, obtained by whole milk separation. The membrane method in the processing of secondary dairy raw materials allows for an environmentally-friendly waste-free production. It is a promising trend in the modern food industry: it creates opportunities for a large range of novel dairy products, beverages, and animal feed, as well as for other sustainable technologies. The paper describes how the volume of permeate flux mass transfer and the selectivity of polysulfonamide ultrafiltration membranes (PSA-20 and PSA-50) depend on the volume of operating load and circulation rate during whey and skimmed milk separation. The authors analyzed the mass transfer and the hydrodynamics in the channel of a roll type baromembrane, including the gel formation process. They established the influence of the milk solids weight ratio in the liquid polydisperse system on the permeate flux volume and the selectivity of the polysulfonamide ultrafiltration membrane (PSA-50).

Ключевые слова

Milk whey, membrane technology, ultrafiltration, permeate flux, membrane selectivity

ВВЕДЕНИЕ

Whey is a byproduct of curds, cheese and casein. It contains up to 50% of whole milk solids [8, 9], which makes it a valuable secondary raw material. However, whey is often treated as production wastes and discharged into the environment, thus causing serious environmental damage [8, 9]. Such type of dairy wastes can be recycled by ultrafiltration. Unfortunately, baromembrane separation of whey is not profitable for medium and small milk processing plants [8, 9]. Nevertheless, it is possible to increase the process efficiency by rationalizing it.

When whey is ultrafiltrated with the maximum permissible value of the concentration factor, the permeate flux through the polymer membrane can be increased while maintaining a specific selectivity index.

The current research provides a theoretical and experimental justification of the main operating parameters and the maximum permissible value of milk solids content in whey and skimmed milk during their separation by ultrafiltration.

ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ

The experiment involved whey, obtained as a byproduct of cottage cheese processing, and skimmed milk, obtained by whole milk separation. Tables 1 and 2 feature the basic physicochemical characteristics of the dairy raw material and the operational parameters of the polymer membranes. A scientific data analysis [8, 9] and an analysis of the authors’ own research [1–4, 8] have made it possible to establish that the best option available for ultrafiltration separation of secondary dairy raw materials are polysulfonamide ultrafiltration membranes PSA-20 and PSA-50 produced by Vladipor (ZAO STC Vladipor), Russia.

According to the main parameter (extreme delay), these membranes can be used for ultrafiltration of any dairy raw material. Under the same conditions, the difference between polyamide membranes and cellulose acetate ones lies in their extended service life and greater cost. However, PSA membranes allow for a more rigid washing and a higher operating pressure. The process of tangential ultrafiltration was carried out in a special laboratory installation. The surface area of the membrane was < 0.5 m2 . The operating pressure, the circulation rate of the liquid polydisperse system in the baromembrane channel, and its temperature varied in the following ranges: ∆Р = 0.1–0.4 MPa, V = 0.05–0.45 m/sec and t = 8–18°С accordingly. The permeate flux volume Q and the selectivity of the PSA-20 and PSA-50 membranes Ψ were determined experimentally. The Ψ index was calculated by the following formula:

where: V1 – initial volume of the separated system; С1 – the mass fraction of dispersed particles; V2 and С2 – the volume of the retentate and the mass fraction of the dispersed particles.

The confidence coefficient of the results obtained is 95%.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Theoretical aspects of mass transfer with gel formation in a roll type baromembrane. The process of baromembrane separation provides maximum use of the membrane surface. To ensure the separation in the tangential flux, manufacturers often use the spiral roll filter element. A simultaneous flux in the axial and radial directions makes it possible to reduce the pressure drop in the liquid system and to reduce the size of stagnant zones in the operating channel [1–3].

Many studies focus on a general description of the fluid motion in thin channels with permeable walls [1–3, 12]. However, the flux in the roll type baromembrane channel has a distinct feature: the trajectories of the particles of the fluid are curvilinear, which means that they are influenced by the centrifugal force. This aspect should be taken into account when developing a mathematical description of its hydrodynamics.

A system of equations to describe the steady flow with a constant viscosity coefficient should include the Navier-Stokes equation and the continuity equation in the projections on the axis of the cylindrical coordinate system.

In the following equation, r is the curvature radius of the membrane channel at its inlet; b and h – the halfwidth of this channel in the directions of the axes r and z respectively; w, u, v are the characteristic values of the corresponding velocities Vr, Vv,Vz. To simplify the mathematical expressions, r was replaced with variable y by using the formula r = R + y.

Taking into consideration that 

we proceed to dimensionless variables:

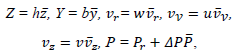
where Pr - the pressure of the liquid system at the outlet from the membrane channel, P – ܲgradient of the operating pressure in the device. The dimensionless parameters wh/(bv) and ur/(Rv) can be equated to 1, in accordance with the principle of least action. Assuming that v = uh/R, while w = ub/R, and taking into consideration that the term that contains the pressure gradient has the same order of magnitude as the terms that include the coefficient of viscosity, it can be written that 

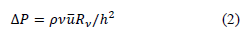
The equation including (small dimensionless parameter) can be solved by power expansion. The first approximation makes it possible to obtain the following system of equations: 

where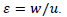 

Taking into consideration that the pressure P of the liquid system is a parameter independent of the vertical coordinate and based on the small value of the parameter ε ,the subsequent simplification of the equation system (3–5) leads to a system of the following differential equations:

We assume that the value of the working pressure P of the liquid system changes significantly only along the length of the channel. Then the radial velocity component Vr will be zero, and the dependence of the longitudinal component Vv on the value of the vertical coordinate will be determined by equation (7). After defining Vv, the vertical component Vz can be calculated by equation (6). To determine the velocity profile of the liquid system for equations (6–9), the following boundary conditions must be introduced:

 

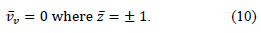
The upper wall of the membrane channel is impenetrable to permeate

 

on the bottom wall 

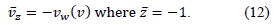
The tangential component: the solution for equation (7) with boundary condition (10) can be written as follows: 

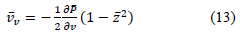
By substituting expression (13) into equation (6) with subsequent integration, we determine that 

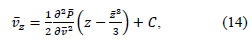
where C – an integration constant that does not depend on the values of the variable z; however, it can be determined by the value of the variable v for the general case. The expression for the constant C can be found by using the boundary condition (11):

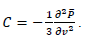
In accordance with 

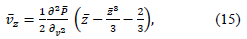
the pressure distribution along the length of the membrane channel as 

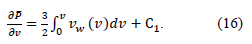
To determine the integration constant С1 , it is necessary to adopt the condition that u is the average flux rate of the liquid system at the entrance to the membrane channel; in this case we obtain the following expression in the dimensionless variables:  

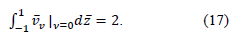
Hence, С1 = 3, which makes it possible to rewrite equation (16) as follows: 

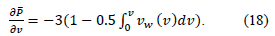
After integrating expression (18), we obtain the following equation that determines the pressure distribution in the liquid: 

The expression can be used to calculate the mass transfer during gel formation on the membrane surface. The expression has a significant effect on the permeate flux and membrane selectivity. 

It should be noted that the parameters of the mass transfer process, complicated by gelling, have already been determined. However, the following convective diffusion equation describes a stationary process only for the cases when the coefficient of molecular diffusion does not depend on the concentration of matter in the liquid system, and only for baromembrane separation of liquid in a straight channel [1–3]: 

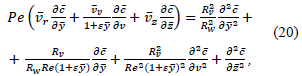
where  – the concentration of the released substance at the entrance to the baromembrane channel, сд – concentration of gel formation; Pe – Peclet number, calculated according to the penetration speed and half-height of the membrane channel.

However, if in equation (20) we assume that    (where and ) while considering the approximation  then the convective diffusion equation can be simplified and written as follows:

Considering the connection (18), velocity  components Vz and Vv in equations (13) and (15) can be represented as

Since the ultrafiltration process usually involves  very small values of the molecular diffusion coefficient  D (in comparison with the reverse osmotic membrane  separation), then Pe ≫ 1. And that means that the  change in the concentration of the substance released  on the membrane occurs only in the thin diffusion  perimembrane layer. Proceeding from this, one can  further transform equation (21) by introducing a new  independent variable ŋ instead of z:

Assuming that for the thin diffusion perimembrane layer ŋ ≪ 1, equations (22) and (23) can be simplified and presented as follows: 

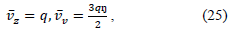
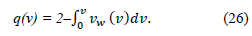
Hence, the final equation to define the concentration will be 

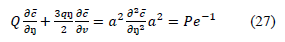
The boundary conditions for equation (27) will be

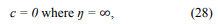
because outside the zone of the diffusion perimembrane layer (where ŋ = ∞) concentration с of the substance on the membrane equals its concentration at the entrance to the channel Cв:  

which means that the convective flux of the substance on the membrane to its surface must be compensated by its diffusion flux away from the surface (where z=h).

Assuming that the concentration of the substance on the membrane is equal to the concentration of gel formation, equation (29) can be rewritten in dimensionless variables:

By introducing the dimensionless variable

we solve equation (27) with the given boundary conditions (28) and (30). Thus, 

with boundary conditions 

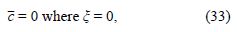
in expression (32)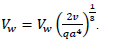  

Differential equation (32) with boundary conditions (33) and (34) can be solved as follows: 

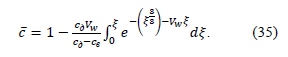
Multiplier Vw is defined from the condition 

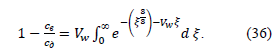
Thus,  the  performed  analysis  of  the  laws  of hydrodynamics and mass transfer established that the calculation of the membrane element of a roll type baromembrane reduced itself to determining the concentration of the substance at the membrane outlet with the help of equations (34), (36) and the equation of material balance.

The modern popular methods of mathematical description of transmembrane mass transfer during membrane filtration have a number of significant limitations, which substantially narrows their practical use since they cannot be applied directly to whey ultrafiltration. Hence, the main operating parameters of the process have to be determined experimentally in order to approbate the results obtained theoretically. The experiment allowed the authors to conclude that PSA-20 and PSA-50 membranes were especially effective in the ultrafiltration separation of skimmed milk and whey.

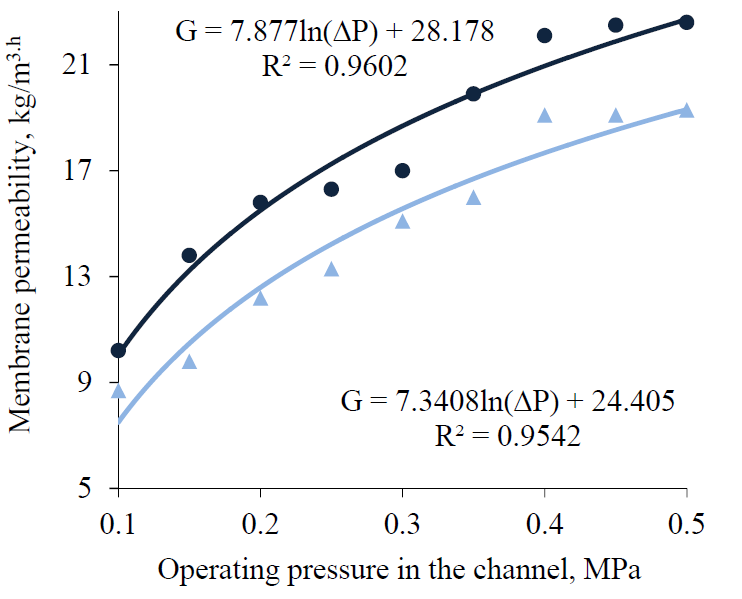
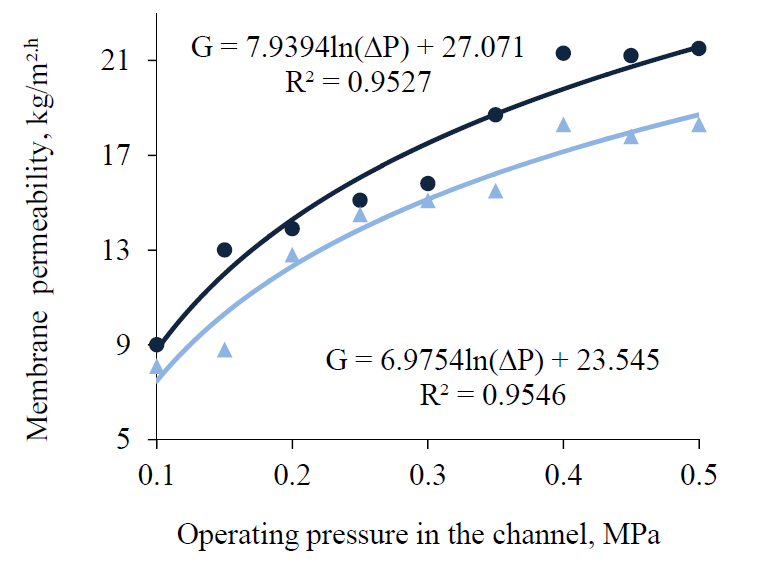
Dependence of the permeate flux and the selectivity of PSA-20 and PSA-50 membranes during whey and skimmed milk ultrafiltration on the operating pressure and circulation speed of the separated system in the baromembrane channel. The driving force of the ultrafiltration process in polydisperse liquid systems is the transmembrane pressure Δp [1–3, 7, 10, 11]. Therefore, at the first stage of the studies, the authors determined experimentally the dependences of the permeate flux G of the preselected membrane types on the pressure Δp in the circulation loop of the ultrafiltration device at constant values of other process parameters. Fig. 1 and 2 show graphs of functions of G = f(Δp) type for membranes PSA-20 and PSA-50, obtained by whey and skimmed milk ultrafiltration.

The analysis of the experimentally obtained dependences of G = f(Δp) type revealed an identical change in the permeate flux through PSA-20 and PSA-50 membranes: the growth of G in the channel of both membranes was proportional to the increase in operating pressure. However, tgφ= dG/dΔp of the graphs for skim milk was lower than that for curd whey. Since the physical significance of tgφ is the rate of the increment of the function G = f(∆р), it can be concluded that in whey ultrafiltration the permeate flux through the membrane G and its intensity increase. This phenomenon can be explained by the fact that the physicochemical composition of skimmed milk by mass fraction of milk solids is 2–3% higher than that of whey.

The analysis of the graphs of G = f (Δp) function revealed that a significant increase in the permeate flux through membranes occurs under the same conditions when the operating pressure rises from Δр = 0.15–0.17 MPa to Δр = 0.32–0.34 MPa. From further on, parameter G virtually does not change. When the Δp parameter rises up to 0.44–0.46 MPa during skimmed milk ultrafiltration, it produces a slight effect on the permeate flux. In case of whey ultrafiltration, G tends to decrease. Based upon the position of the sieve model of the ultrafiltration separation process, a significant increase in membrane selectivity at Δp > 0.44–0.46 MPa is probably associated with the mechanical blocking of pores by protein particles, complicated by the deformation of the membrane structure to some extent, which reduces the initial size of the flow area of the pore space. This suggests that the choice of the optimal region of the operating pressure in the membrane channel should be limited by the range Δp = 0.32–0.42 MPa.

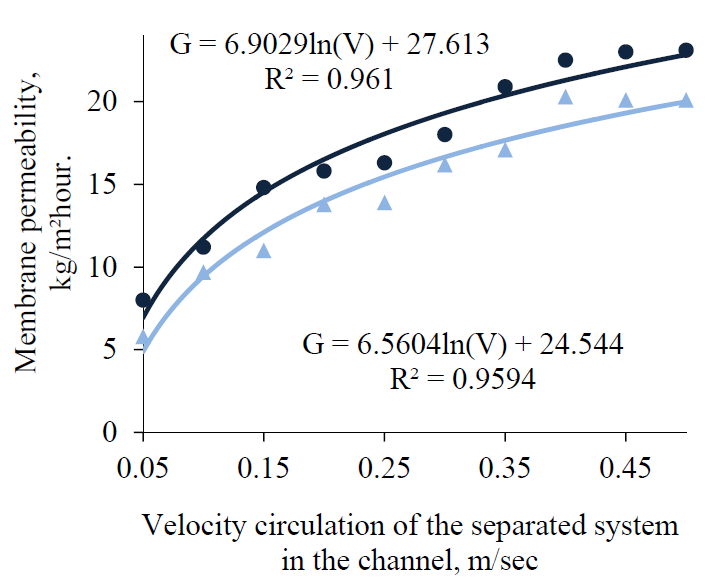
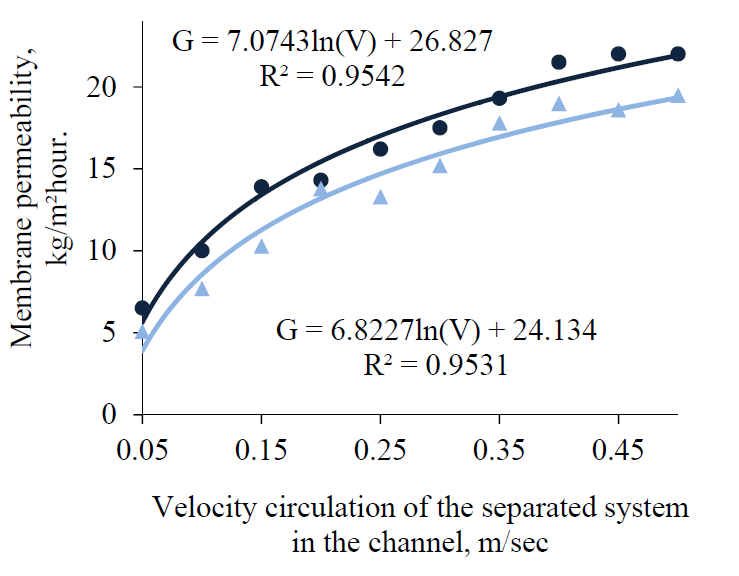
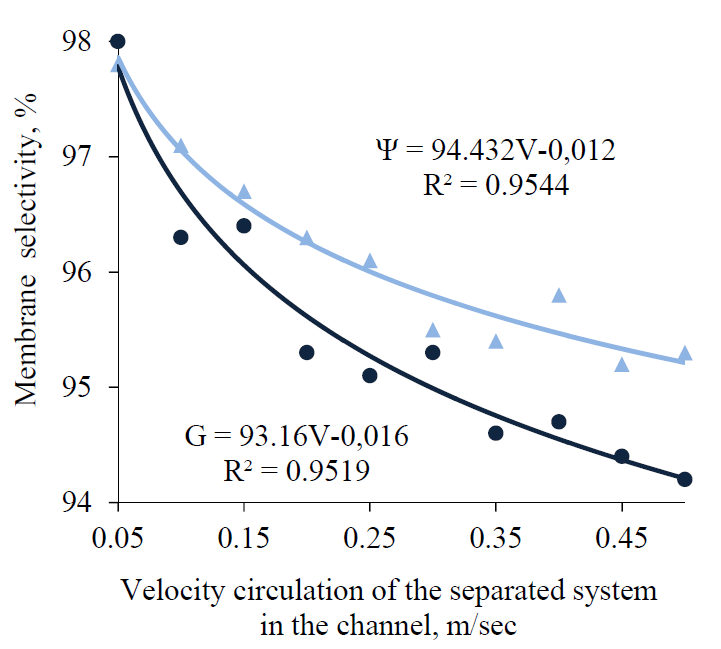
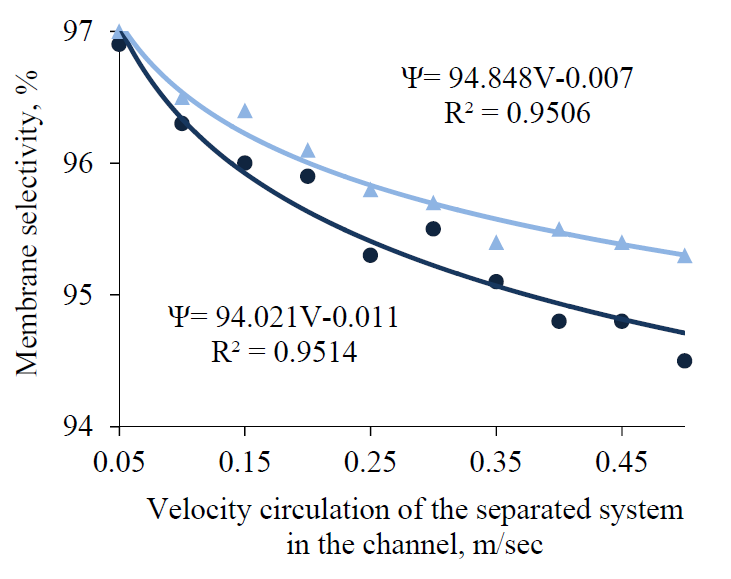
 It should be taken into account that the selectivity and the value of permeate flux through the membranes in the tangential flow of the separated liquid medium in the baromembrane contour is influenced by the circulation velocity index V (m/sec), in addition to the operating pressure. Graphical dependences G = f(V) and Ψ = f(V) for PSA-20 and PSA-50 membranes were obtained experimentally by ultrafiltration of curd whey and skimmed milk (Figs. 2 and 3, Figs. 4 and 5 correspondingly). 

The analysis of the graphical dependencies G = f (V) and Ψ = f (V) shows that a significant increase in the permeate flux through the membrane is accompanied by an increase in the circulation rate of both curd whey and skimmed milk, within the range V = 0.16–0.36 m/sec If the sieve model of the ultrafiltration process is taken into account, an increase in membrane selectivity Ψ at V > 0.3 m/sec can be explained by the fact that the unstable deposition areas on the membrane surface begin to degrade in the membrane channel at a given circulation speed [5–8]. However, if this parameter grew more than V = 0.3 m/sec in the laboratory device, it was insufficient to remove stable protein fields on the membrane surface [3–7, 10]. This conclusion is supported by the fact that if velocity was increased more than V = 0.3–0.4 m/sec during skimmed milk ultrafiltration, this had almost no effect on the permeate flux through the membrane. And in the case of curd whey, there was a slight tendency to the increase of G, which weakened the intermolecular bonds in the ‘membrane – dispersed particles’ system. Thus, it can be concluded that the optimal range of the circulation velocity of whey in the baromembrane channel should be limited by the range V = 0.2–0.3 m/sec.

The performance of membrane instalments in industry has demonstrated that the efficiency of the filtration process of secondary dairy raw materials under identical conditions depends on the optimum value of parameter V. This opinion was voiced in a number of papers [1, 9, 10–12] that featured the deposition of dispersed particles on the membrane. It should be noted that cleaning and subsequent regeneration of the membranes can be an important operating parameter of the baromembrane equipment, depending on the contamination of the membrane surface. 

The basic requirements usually imposed on baromembrane plants are their high productivity and the minimum membrane volume to membrane surface area ratio. However, it is the end product manufacturing technology that determines both the permissible selectivity index and the parameters of the permeate flux volume and filter elements, which are subject to certain requirements, i.e. the acceptable cost of membranes, their chemical resistance to detergent components, etc. Thus, a high level of permeate flux with a sufficient degree of membrane selectivity should be ensured by the optimal parameters of ultrafiltration of the secondary dairy raw materials. Curd whey is a complex high-molecular polydisperse system. During its baromembrane separation, membrane selectivity and permeate flux are significantly influenced by the level of concentration polarization [1–3, 9–11]. This phenomenon raises the particle concentration in the separated system from the initial value of С0 to Сmax. As a result, deposition areas begin to form on the membrane surface, which significantly reduces the permeate flux through the membrane and might block the pores completely. In this case, the concentration polarization level is characterized by the ratio of the dispersed particle concentrations С0 directly at the surface of the membrane С1. But in general, С0 increases with time, and a constant level of concentration polarization can be maintained only by decreasing С1. 

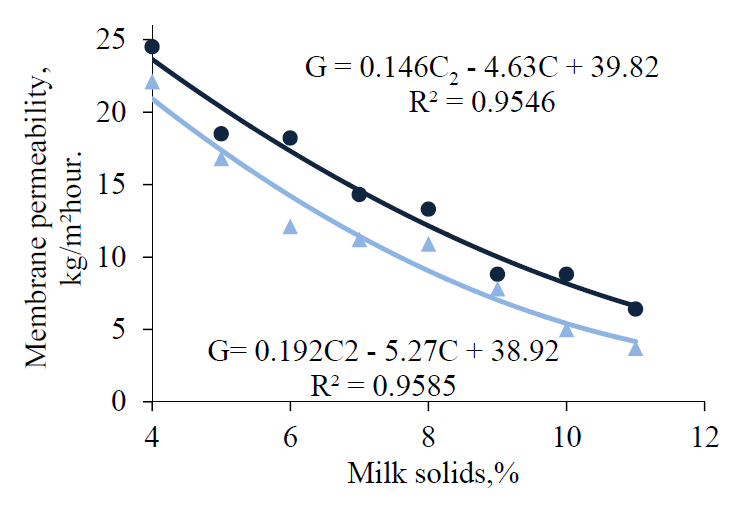
Dependence of the influence of the mass fraction of milk solids on the permeate flux and membrane selectivity. The selectivity and the volume of permeate flux are also affected by the complex state of the dispersed particles. Thus, under the same conditions, the efficiency of membrane filtration of skimmed milk and whey ultimately depends on the milk solids weight ratio in the retentate, since this indicator can accurately estimate the level of concentration of protein particles caught in the membrane. If ultrafiltration is carried out according to periodic pattern, the milk solids weight ratio will increase with time, together with the level of concentration polarization in the perimembrane zone [5, 6–8]. Many authors [1–5] claim that if the retentatene includes a certain amount of finely dispersed particles that are denser than those of casein dust, the permeate flux may increase, and the membrane selectivity may fall. However, in this case it is necessary to create a high-speed flux therein [1], which is most beneficial in tubular type installations. Therefore, the membrane selectivity and the permeate flux volume, which determine the ultrafiltration efficiency, are likely to depend on some maximum acceptable value in the separated system of milk solids. The analysis of characteristic curves (Figs. 1–6) revealed the similarity in the changes of the main parameters of PSA-50 and PSA-20 membranes. Figs. 7 and 8 show the results of experimental studies in the form of characteristic curves G = f(DM) and Ψ = f(DM). Therefore, at this stage of the study, it is possible to use only PSA-50 membrane, in which G is higher than in PSA-20.

As for skimmed milk ultrafication, it was established that the reduction rate value of the permeate flux dG/dMS significantly decreased when the index of milk solids weight ratio reached DM = 8.6–8.9%. However, when DM > 9.2%, this parameter approaches zero. In the case of whey ultrafiltration, dG/dMS tends to zero at DM ≥ 10%. The growth rate of the membrane surface selectivity dΨ/dMS also decreases both during the filtration of skimmed milk and curd whey, assuming its minimum value in the range DM = 8.6–9.9%. If the milk solids weight ratio in the retentate exceeds DM = 10.2–10.4% during whey separation, membrane parameter Ψ reaches 97.5%, and G sinks to 3–5 kg/m² hour.  

ВЫВОДЫ

During ultrafiltration of secondary dairy raw materials, a membrane selectivity index higher than 96.0–96.5% is considered economically impractical [1]. Hence, the limiting value of this parameter is MS = 10.0% during curd whey baromembrane separation through a roll type PSA-20 membrane. However, if we take into account the recommendations in [13], then MS should not drop below 20% for milk protein concentrates. This can be achieved by thickening the ultrafiltration retentate in a vacuum evaporator with subsequent semi-finished goods production. At the same time, it is possible to use a less concentrated liquid retentate, e.g. milk drinks [13].
Theoretical calculations of MS (34–36) are similar to those obtained by experimental data. Still, it is necessary to take into account the physicochemical properties of the system, which have a significant effect on the permeate flux and membrane selectivity [1]. It should be noted that very a strong complex deposition appears on the membrane surface when MS = 10.0% during whey ultrafiltration [1]. The stagnant zones in the membrane channels trigger the development of microflora both in the retentate and in the permeate. These factors, together with the physicochemical properties of the system, determine the reduction rate of the permeate flux during baromembrane separation of liquid polydisperse systems. In this regard, it is of great importance to clean membranes from surface contaminants. This ensures the reliability of baromembranes during the ultrafiltration separation of secondary dairy raw materials. However, to determine the optimum parameters of regeneration and washing, a separate experimental research is required. 

КОНФЛИКТ ИНТЕРЕСОВ

The authors declare that there is no conflict of interest related to this article. 

БЛАГОДАРНОСТИ

The authors would like to express their deepest gratitude to the staff of the laboratory ‘Units Operation in Food Engineering’ of the Institute of Life Sciences, North Caucasus Federal University, for the help they provided in conducting the experimental studies. 

ФИНАНСИРОВАНИЕ

North Caucasus Federal University. 

СПИСОК ЛИТЕРАТУРЫ

1. Babenyshev S.P., Emelʹyanov S.A., Zhidkov V.E., et al. Theoretical aspects and mathematical model of Process membrane division liquid highmolecular systems. Agricultural Bulletin of Stavropol Region, 2015, vol. 2, no. 18, pp. 7–11. (In Russ.).
2. Baranov S.A. Optimizatsiya raboty ustanovok membrannoy filʹtratsii [Optimization Performance of Membrane Filters]. Milk Processing, 2013, vol. 4, no. 160, 37 p. (In Russ.).
3. Lobasenko B.A. and Semenov A.G. Manufacture of milk proteins using membrane ultrafiltration with separate selection of the concentrate. Achievements of Science and Technology of AIC, 2009, no. 5, pp. 65–67. (In Russ.).
4. Ponomarev A.N., Kluchnikov A.I., Merzlikina A.A., et al. Kinetics of ultrafiltration cheese whey. Dairy Industry, 2016, no. 4, pp. 78–79. (In Russ.).
5. Rebezov M.B., Zinina O.V., Nurymkhan G.N., et al. Secondary raw materials of the Diary industry: the current state and prospects. Agro-Industrial Complex of Russia, 2016, vol. 75, no. 1, pp. 150–155. (In Russ.).
6. Rytchenkova O.V. Issledovanie protsessa vydeleniya belkov iz kontsentrata molochnoy syvorotki [Protein Segregation from Whey Concentrate]. Journal Advances in Chemistry and Chemical Technology, 2008, vol. 22, no. 13, pp. 73–76. (In Russ.).
7. Khramtsov A.G. The regularities of forming molecular-sieve separation of milk protein-carbohydrate raw materials for next-generation products (to jubilee of Professor I.A Yevdokimov). Newsleter of North-Caucasus State Technical University, 2015, vol. 5, no. 50, pp. 197–204. (In Russ.).
8. Kovasin K. Modeling Ultrafiltration and Filtration Phenomena Applied in Chemical Pulping Processes. Helsinki: Helsinki University of Technology, Laboratory of Chemical Engineering and Plant Design, 2002. 52 p.
9. Leung W.F. and Probstein R.F. Modeling of mass transfer in the ultrafiltration of spent sulfite liquor. Industrial and Engineering Chemistry, Fundamentals, 1979, vol. 18, no. 3, pp. 274–278.
10. Melnikova E.I., Losev A.N., and Stanislavskaya E.B. Microparticulation of caseic whey to use in fermented milk production. Foods and Raw Materials, 2017, vol. 5, no. 2, pp. 83–93. DOI: https://doi.org/10.21179/2308-4057-2017-2-83-93.
11. Sedelkin V.M., Surkova A.N., Pachina O.V., et al. Simulation of membrane ultrafiltration of secondary raw milk. Petroleum Chemistry, 2016, vol. 56, no. 4, pp. 367–378. DOI: https://doi.org/10.1134/S0965544116040095.
12. Wang Y., Qu H., and Mo D. Measurement of pore diameter and filtration performance of nuclear track membranes. He Jishu/Nuclear Techniques, 2016, vol. 39, no. 1, pp. 010501. DOI: https://doi.org/10.11889/j.0253-3219.2016.hjs.39.010501.
13. Babenyshev S.P., Mamay D.S., Chernov P.S., et al. Sposob polucheniya molochnogo fruktovo-ovoshchnogo napitka [Technique for Producing a Milk Drink of Fruit and Vegetable Juices]. Patent FR, no. 2489891.