Аннотация

The kinetics of the drying process in continuous drum dryers differs from the drying of single objects in a batch mode. Drying process is affected by too many factors; hence, it is practically impossible to obtain an analyt- ical solution from the initial equations of heat and mass transfer, since the duration of drying depends on the opera- ting parameters. Therefore, it is of high theoretical and practical importance to create a highly efficient rotary drum dryer. Its design should be based on an integrated research of non-stationary processes of heat and mass transfer, hydrodynamics of fluidized beds, and drying kinetics in the convective heat supply. The experiment described in the present paper featured sunflower seeds. It was based on a systematic approach to modelling rotary convective drying processes. The approach allowed the authors to link together separate idealized models. Each model characterized a process of heat and mass transfer in a fluidized bed of wet solids that moved on a cylindrical surface. The experiment provided the following theoretical results: 1) a multimodel system for the continuous drying process of bulky mate- rials in a fluidized bed; 2) an effective coefficient of continuous drying, based on the mechanics of the fluidized bed and its continuous dehydration. The multimodel system makes it possible to optimize the drying process according to its material, heat-exchanger, and technological parameters, as well as to the technical and economic characteristics of the dryer.

ВВЕДЕНИЕ

The general theory of heat and mass transfer in capillary porous and other dispersed media belonged to Prof. Lykov. It was based on the thermodynamics of irreversible processes and the theory of generalization of variables. According to Prof. Lykov, sets of equations are to be solved as a single complex process [1].

The theory of heat and mass transfer is based on solving sets of linear equations with boundary conditions, which corresponded to constant and variable potentials in a medium that varied according to established laws. Thus, it was intended for stationary material and medium [2].

To intensify and improve technological processes, one needs reliable, physically valid modelling methods [3]. This is especially important for energy-intensive drying processes of wet solids in a fluidized bed that is moving along a cylindrical surface, e.g. drum dryers [4].

In this paper, modelling means a physical analysis of heat and mass transfer, as well as the hydrodynamics of the processes that occur a rotary drum dryer, their mathematical description, and possible solutions by analytical or numerical methods involving various software [5]. The analytical and numerical methods were based on preliminary data on the kinetics of drying and heating of individual particles. Such information was obtained either from the available model representations or from experimental data. In most cases, preference was given to direct experimental data, which took into account possible effects of anisotropy of heat and mass transfer properties and irregular geometric shape of particles of real solids.

An adequate description of the continuous drying technology of wet solids in a fluidized bed requires an integrated approach to the problem. Such an approach requires a system analysis of hydrodynamic, diffusion, and thermal processes complicated by an overlap of various phenomena. A complete theoretical picture of a continuous drying process should be based on a mathematical model that would link a set of typical structures, or idealized models, each of which reflects a particular type of transfer or transformation. The optimal way to develop a new drying technique is to combine the multimodel system of drying processes with experimental studies on the kinetics of moisture removal in a fluidized bed [6].

The research objective was to develop a multimodel system for the continuous process of drying and heat transfer in a fluidized bed of wet solids.

ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ

The study was based on a complex of general and specific scientific methods. The general scientific methods involved analysis and synthesis, testing a theory with practice, interpretation of the results obtained, etc. The specific scientific methods included the abstract logical method, the method of modelling, the empirical method, the method of statistical probability, etc. The theoretical and methodological foundation of the research included studies conducted by Russian and foreign experts in the field of drying, such as Ginzburg, Frolov, and Lykov.

The research featured sunflower oil seeds.

The thermophysical characteristics of the vegetable raw material were determined according to the non-stationary thermal mode method of two temperature-time points developed by Volkenstein. The method of differential thermal analysis was used to identify the intervals of temperature zones of moisture evaporation with different forms and energy of moisture binding with the material. It was accompanied by the method of differential scanning calorimetry, which was used for quantitative measurement of heat flows that occurred when the trial sample and the control sample were undergoing a simultaneous programmed heating. The methods of high-performance gas chromatography, atomic absorption spectroscopy, infrared spectroscopy, capillary electrophoresis, and acid hydrolysis were used to determine the content of vitamins, amino acids, and other quality indicators of the wet solids. The measurement errors did not exceed the values established in the current standards for quantitative analysis of the quality indicators of the wet solids. The main part of the theoretical and experimental research was carried out on the premises of the Voronezh State University of Engineering Technologies (Voronezh, Russia) and the Bobrovsky Vegetable Oil Plant (Bobrov, Russia).

The research objective was achieved by the synthesis and analysis of classical and novel analytical and empirical methods in the sphere of heat and mass transfer and food dehydration studies. The obtained relations, the approximating equations, and the simulation results corresponded with the experimental data. The measurement results underwent statistical processing. The procedures and design solutions did not contradict the established methods of rational design and engineering. Modern computer mathematical programmes, instruments, and authentic trial equipment were used to conduct the experiments and test the physical and mathematical models of the drying and steam treatment processes.

The systematic approach in modelling the convective drying processes. The process of continuous drying is an original research subject that can be marked as a certain system S, while the model of the drying process M represents a different system. According to the systematic approach principle, the drying process interacts with the external environment E. Depending on the research objective, the study may feature different ratios between the subject and the external environment. These relations represent a model of relations of the external environment with the subject. Since our ideas of the subject and the external environment are also models, the following models can be proposed: M_S is the model of the subject S, M_F is the model of external environment at the inlet, M_T is the model of external environment at the output, M_FS is the model of the connections between the external environment and the subject at the inlet, and M_ST is the model of the connections between the external environment and the subject at the output.

The combination of all these models

forms a multimodel system of transfer phenomena (Fig. 1).

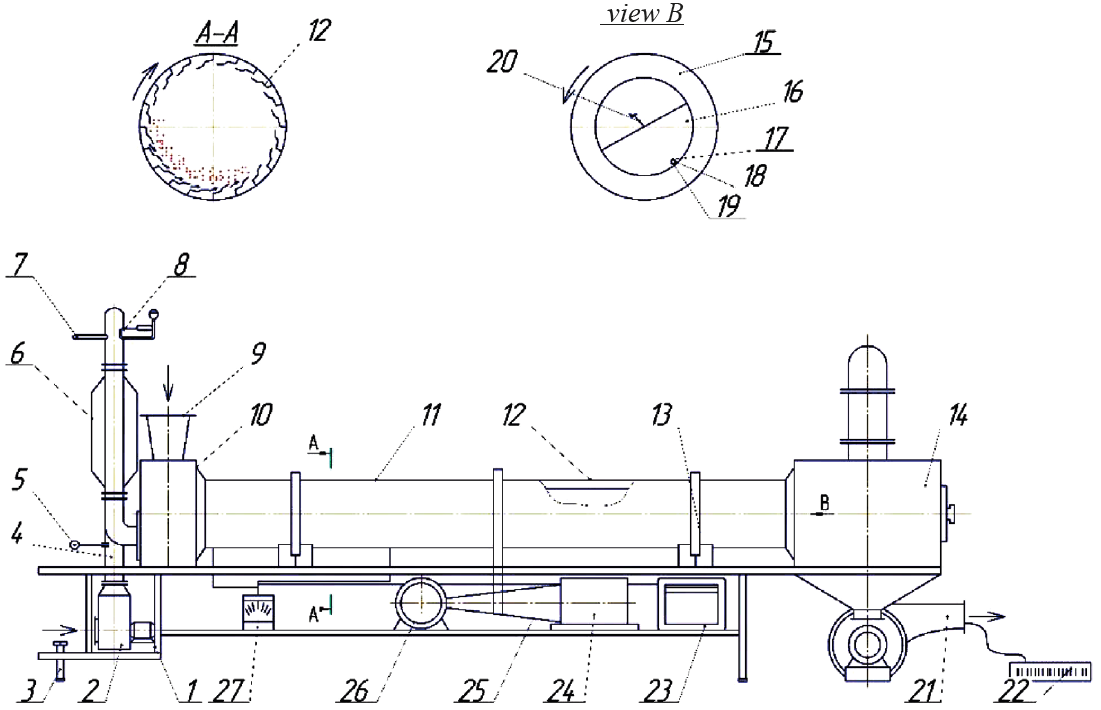
A drum dryer as a subject of system modelling of non-stationary processes. Fig. 2 shows the experimental drum dryer used in the study of the continuous drying process.

The pressure type fan (2) was fixed on the angular steel frame (1). The fan was designed to supply atmospheric air through the duct (4) into the heater (6). The heater consisted of several sections. The flow rate of the air supplied to the heater was regulated by means of the gate valve (5). The temperature and the relative humidity of the air entering the drying chamber were measured with the dry (7) and the wet (8) thermometers.

At the core of the whole design there was a steel drum (11) with a diameter of 0.3 m and a length of 1.3 m. On the inner surface of the drum there was the channel nozzle (12). The nozzle contained longitudinal slots to feed the drying agent to the bed of wet granular material. The drying drum (11) was supported by two pairs of rollers (13). It was driven by the electric motor (26) and the gearbox (24), which were kinematically interconnected by the chain transmission (25).

During the drying process, the drying agent was supplied directly to the zone of the channel nozzles under the dryable material.

The pipe (9) was assembled on the body of the loading chamber (10). The pipe fed the wet bulk material to the drying drum. The spiral rotation of the drum moved the material to the discharge chamber (14).

The retaining ring (15) was assembled on the end surface of the drum. The ring slid in the groove of the fixed flange (16), through which the bulk material was continuously unloaded. During the drying process, the interior of the drum (11) was under a slight negative pressure due to the fact that the performance of the fan (21), which took away the waste drying agent, was several times higher than that of the delivery fan (2).

The temperature control of the drying agent was carried out directly in the bed of the wet solids. The thermocouples (17, 18, and 19) were installed on the bracket (20) (Fig. 2, view B).

The temperature was recorded with the electronic automatic self-recording potentiometer (23).

The relative humidity of the waste drying agent was measured with the hygrometer (22), a sorption-frequency single-channel digital device. The semiconductor thermoanemometer (27) measured the speed of the drying agent at the inlet and the outlet of the drum, as well as above and below the surface of the bed.

The angle of the drum, the frequency of its rotation, and the speed and temperature of the drying agent were set at the initial stage of the experiments. After that, there began a continuous supply of proportioned wet bulk material. Over the next 60–70 min, the material was sampled to measure its thermophysical characteristics, while the process of wet material feeding continued in the same mode.

After the sampling, the feeding of the wet bulk material to the drying drum and the movement of the drum stopped simultaneously. The speed and the temperature of the drying agent remained constant, according to the experimental conditions. After that, all the material was discharged from the drum into the receiving container, and its volume and weight were measured.

Taking into consideration the design feature of rotary drum dryers and the methods of continuous drying of wet solids in a fluidized bed, the model of continuous drying process can be represented as a multimodel system of transfer phenomena (Fig. 3).

The continuous drying process as a system of transfer phenomena. The model of the continuous drying process of wet solids in a fluidized bed displays the properties of the material and the coolant and the nature of non-steady processes that occur in the fluidized bed. It also makes it possible to improve the drying at various initial parameters of the material and the coolant.

The model of the product subjected to drying and the coolant connects the model of the system with the external environment and control actions. It also calculates the properties of the material and the coolant.

The following models of transfer phenomena correspond with the continuous process in a rotary drum dryer (Fig. 3):

– the model of the product subjected to drying;

– the coolant model;

– the model of the movement of the wet solids on the cylindrical surface;

– the model of the coolant fed to the fluidized bed;

– the hydrodynamic model of the fluidized bed;

– the model of the complex heat and mass transfer;

– the model of the drying process in the fluidized bed; and – the model of the technical and economic characteristics.

The model of the product subjected to drying. If we consider the wet product as a subject of drying with its moisture content, temperature, density of individual particles, and average linear dimensions, we can construct a mathematical model of the technological properties of the bulk material [8]. The model can describe the physical properties necessary for hydrodynamic and heat transfer processes. In this case, the linear dimensions of the bulk material determine its volume, surface area, equivalent diameter, sphericity (non-sphericity) coefficient, and the specific surface area. The equilibrium moisture, angle of repose, and the bulk density of the wet solids are determined depending on their humidity and the moisture of the drying agent. The specific heat is determined depending on the temperature of the product.

The model of the product subjected to drying. Let us consider the wet solids as a subject of drying, characterized by moisture content, temperature, density of individual particles of the product, and average linear dimensions. By doing so, we can construct a mathematical model of the technological properties of the wet solids [8]. The model describes the physical properties necessary for conducting hydrodynamic and heat transfer processes. In this case, the linear dimensions of the bulk material are determined by its volume, surface area, equivalent diameter, sphericity coefficient (non-sphericity), and the value of specific surface. Equilibrium moisture, angle of repose, and the bulk density of the wet solids are determined depending on their humidity and the moisture of the drying agent. The specific heat depends on the temperature of the product.

The coolant model. The wet and heated atmospheric air is considered as a binary mixture of the components of dry air and steam [9]. The parameters of the drying are calculated by the method of superposition of the component parameters. Tables and various functional and empirical relations are used to calculate the parameters of the components.

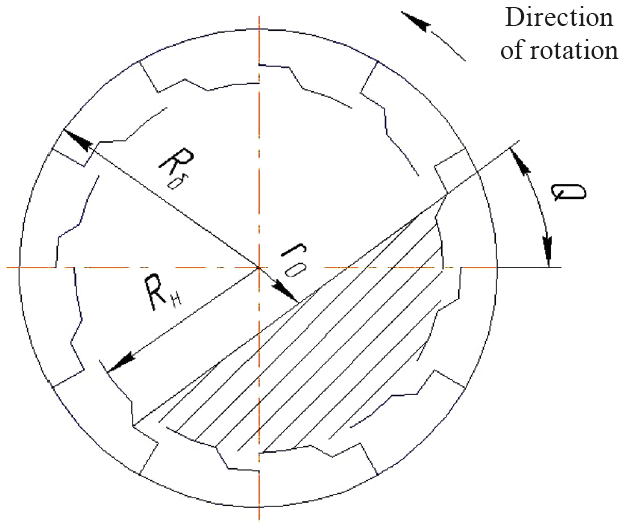
The model of the movement of wet solids on the cylindrical surface. In drum dryers, the material is dried in a fluidized bed while it is purged with a drying agent [5]. Fig.4 shows the flow chart of the bulk material in the transverse direction.

The angle of the bed in the cross section is determined by the angle of repose of the bulk material. It is assumed that the trajectory of the particles passes along a radial arc, whose radius equals the distance from the axis of the drum. When the particle gets to the end of the arc and surfaces, it falls down along the chordal surface of the flow.

The particle moves in the axial (translational) direction only if the flow surface has a certain axial angle, i.e. when there is a difference in the levels of the bed at the inlet and the outlet holes of the drum.

During translational motion, the trajectory of the particle follows the chordal plane. In this case, the trajectory is not perpendicular to the axis of the drum: it forms a < 90° angle with it and is perpendicular to the plane passing through the middle of the chords.

The model of the coolant fed to the fluidized bed. The drying agent enters the drying chamber of the drum dryer through the channels formed by the channel nozzles [6] and the outer cylinder of the drum through the side cavity of the drum (Fig. 5).

The side cavity of the drum was divided by a partition in such a way that the drying agent entered the channels under the nozzles that are situated under the material while the drum is rotating. The channel nozzle has a gap of constant width. The drying agent enters the drying chamber through this gap and contacts the layer of dispersed material.

Thus, the task is reduced to the calculation of gas distribution with an outflow through the lateral permeable surface, i.e. the layer of the dispersed material. It is possible to make an assumption that the parameters of the drying agent and the height of the bed are constant. Thus, one can calculate the hydrodynamics of the flow of the drying agent. In this case, the bed height may be its height in the middle section of the material flow. The parameters of the drying agent, such as density and kinematic viscosity, are assumed to be constant.

Two models were considered when choosing the mathematical model for the coolant supply from the channel nozzle slit through the bed of dispersed material. The first was the model for calculating the distribution of velocity and pressures along the z-shaped collectors; the second was the model of the constant-section air distributor with a longitudinal slit of constant width.

The hydrodynamic model of the fluidized bed. According to the hydrodynamics of the fluidized bed of the wet solids in rotating drum dryer, the drying agent flows around the particles in the fluidized bed of the granular product and between the particles of the material in the channels [6].

In this connection, we can point out external (flow-around), internal (filtration), and mixed hydrodynamics problem.

When solving the problem of heat and mass transfer, it is necessary to determine the active surface area of the product or the specific surface area of the bed and the speed with which the drying agent flows around the particles.

When solving the problem of the hydrodynamics of a bed, one has to determine the hydraulic resistance of the bed of the dispersed material. It is necessary to know the characteristics of the pore channel of the bed, its coefficient of the hydraulic resistance, and the flow rate of the drying agent in the channel.

For generality, it is assumed that the flow velocity around the particle and the flow speed in the channel are equal and related to the flow velocity in the direction of filtration in the whole liquidized bed by the ratio:

The tortuosity coefficient ξ is calculated as follows:

The bed voidage ε is the ratio of voids between the particles in the layer and the volume of the bed. It can be expressed as the following ratio:

The specific surface of the material particles in the bed can be calculated through the specific surface of the particles S_s and layer porosity ε:

The loss of pressure during the movement of the drying agent through the granular layer can be calculated similarly to the pressure loss in pipelines:

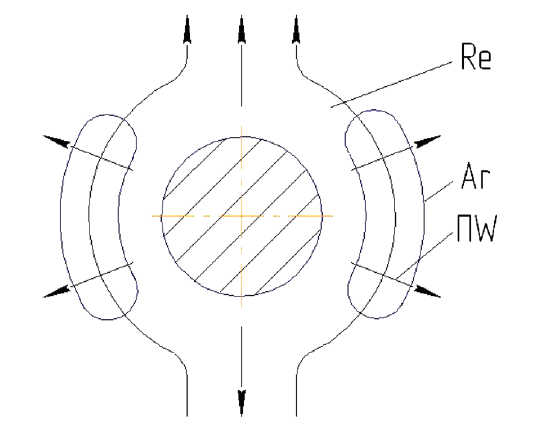
The model of the complex heat and mass transfer. In the general case, when organizing continuous drying of wet solids in a fluidized bed, the coolant is supplied to the drying chamber at the expense of an external heat source (mechanical energy). As a result, there is a continuous forced flow of the heat transfer agent particles around the product. The process of continuous evaporation of moisture from the free surface of the moving material occurs, in this case, in the boundary layer and is caused by velocity and temperature gradients. As a result, there occurs a continuous diffusion flow of the medium. This continuous flow is constantly directed from the surface of the product into the depth of the coolant flow. The difference in the concentration of the vapor-gas mixture near the evaporation surface and in the main heat-wave flow of the coolant leads to a density difference in the vapor-gas mixture. It results in a continuous free natural heat and mass transfer.

Fig. 6 demonstrates the external heat and mass transfer under conditions of continuous dehydration as a combination of simple (marginal) modes of motion: forced, free, and diffusive.

To calculate the simultaneous continuous heat and mass transfer processes, we used the method based on the superposition of the absolute values of Nusselt number [9]. In a complex continuous process, the absolute value of the transfer rate is determined according to the projection values of the transfer rate of simple processes onto two mutually perpendicular planes.

The velocity attitude of the forced motion of the medium U_Re makes an arbitrary angle φ with the planes, in which the velocity vectors of the free motion U_Ar lie.

Fig. 7 shows that the calculated dependence of the forced and the free motion with an arbitrary mutual orientation is

When φ = 0, the forced and the free motions happen in the same plane:

When φ = π/2, the forced and the free motions happen in mutually perpendicular planes:

If the critical geometrical dimensions of the forced and the free motions are the same (L = L_Re = L_Ar), formula (8) coincides with the following relation:

In accordance with the nature of the flow of the medium in the liquidized bed, the calculated relation of the intensity of the continuous transfer of the complex process meets conditions (8) and (10).

The absolute value of Nusselt number in forced motion conditions is calculated by the formula for the ball:

where 1 < Ar Pr < 10₅. In conditions of free motion it is calculated by the formula for the sphere:

where 0,6 < Pr < 8×10³ and Re < 3×10⁵.

In formulae (11) and (12), the critical value is the equivalent particle diameter of the wet solids.

The effective heat transfer coefficient α_er is used as a characteristic of heat transfer intensity. It takes into account the total amount of heat spent on continuous drying in a rotating drum dryer.

The effective heat transfer coefficient α_er is determined by a nonlinear differential equation, presented in dimensionless form:

where y = t – T_i; x = u – u_e; A = αS_s / c_mK; Rb = r(u_i – u_e /[c_m(t – T)] is Rehbinder number.

The solution for the equation (13) is determined by the following power function:

The effective heat transfer coefficient for the fluidized bed of wet solids under continuous dehydration conditions is determined by the following relation:

The model of the drying process in the fluidized bed. Let us consider the general case of an approximate mathematical description of a continuous process of moisture transfer:

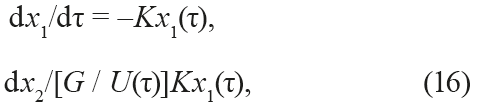
where, in terms of optimal control methods [8], the parameters x₁ and x₂ are phase variables, and U(τ) is the control action.

The system of equations (16) is a combination of the kinetics of the continuous drying and the balance relation ofmoisture in the material and coolant.

Let us define the optimal control Uopt(τ) which transfers the continuous process from

– the given initial state:

– and in the specified final state:

so that the functional assumes the minimum value:

Let us establish a function with auxiliary variables λ₀, λ₁ and λ₂:

and write the system of equations for the function λ₁:

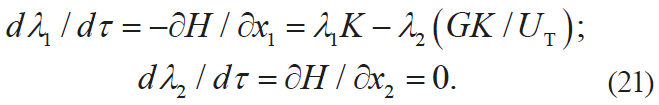
The optimal control of the continuous process results from the condition that the function H has the maximum value:

Thus,

The following function solves the equations of the system (7), which describe the kinetics of continuous drying with the boundary condition (8):

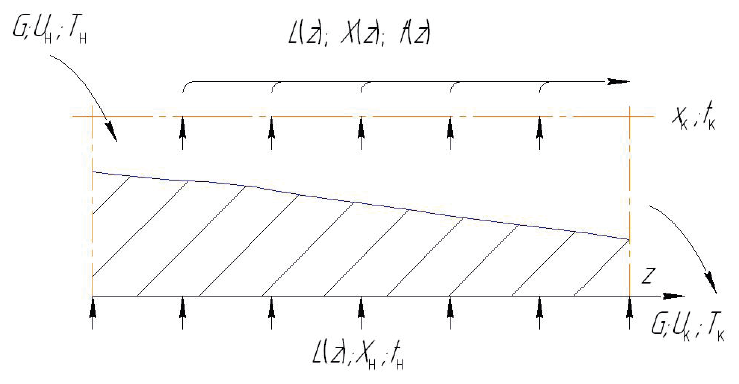
In the rotating drum dryer, the dryable product is, as a rule, continuously loaded into the drying chamber on one side and unloaded on the other. The height of the bed at the input exceeds the height of the bed at the output, due to the rotation frequency and the horizontal angle of the drum. In general, the coolant is fed to the drying chamber and passes through the fluidized bed of the bulk material [5].

To study the dynamics of the continuous dehydration mechanism [9], the original scheme of interaction of the coolant flow and the fluidized bed of the wet solids moving along the cylindrical surface can be presented as (Fig. 8).

For practical calculations, the surface of the fluidized (sliding) bed is represented as a plane, and the cross section of the material flow is represented by a segment of a circle. To describe the continuous drying mode, the continuity equation for the flow of the dryable material can be represented as

Note that the density of the dryable material is the function of its moisture content u:

In rotary drum dryers, the warm-up periods are short, and the drying rate is constant. Hence, the drying rate can be represented as a function of moisture content [10]:

For rotary drum dryers, u = dz/dt. In this case, if we take into account Eq. (25) and Eq. (26), the drying rate can be represented as follows:

The heat is continuously supplied to the dryable product. It heats the material and evaporates the moisture:

In Eq. (29), we point out, first, the heat supplied to the material,

second, the heat spent on heating the mass of absolutely dry material and moisture contained in it,

third, the heat spent on the evaporation of moisture from the material,

Using the continuity equation (25), we express the equation for the temperature of the material through its moisture content:

where

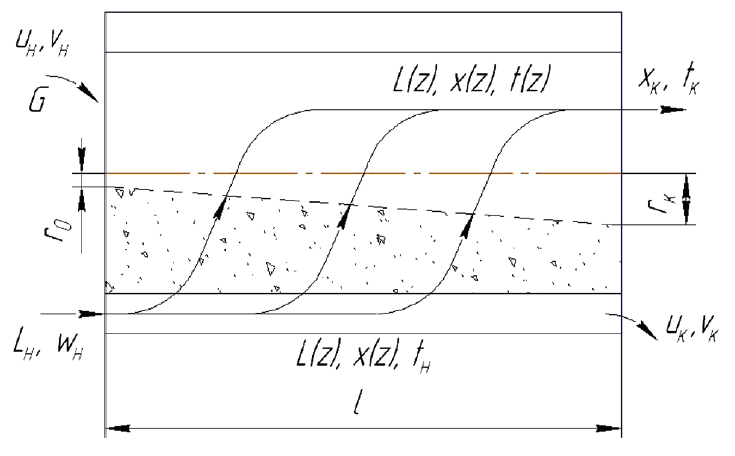
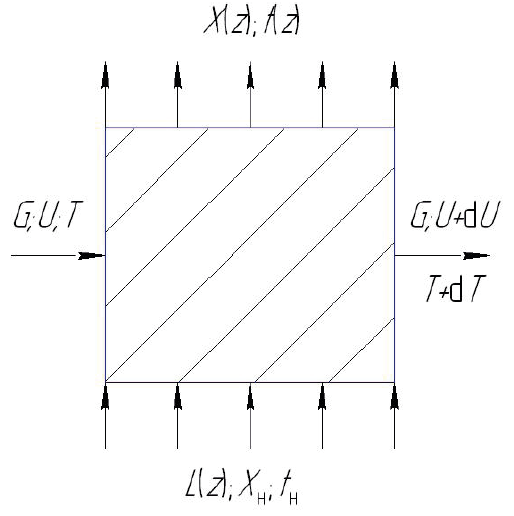
To formulate the balance of the coolant, we divide the fluidized bed of the material of length l into a bed of infinitely small sections of length Δz. Let us assume that, within each of such moving sections, the material is perfectly mixed and has a constant temperature and moisture content. When moving from section to section, the temperature and the moisture contents of the material change to infinitely small values.

Let us single out one of these sections and consider the material flow in the moving element of the wet solids (Fig. 9).

The flow G(1 + u) of the wet solids enters the volume of the moving element, and the flow G(1 + u + du) comes out with its moisture content being u + du. The coolant supplied to the fluidized bed is determined by the expenditure function L(z). When they enter the fluidized bed, the moisture content and the temperature of the coolant are constant throughout the whole layer. They are functions of the z coordinate at the output. The amount of moisture evaporated from the elementary volume of the material equals the amount of moisture absorbed by the coolant that enters the elementary volume:

The heat balance equation is similar to the moisture balance equation (26) for the elementary volume:

where i = (c_m + c_wu) is the enthalpy of the material; I = c_hct + (r + c_st)x is the enthalpy of the coolant; c_hc, c_s is specific heat capacity of the coolant and the steam.

Thus, the continuous drying process on a cylindrical surface can be approximately described by a system of ordinary differential equations:

with initial conditions

and a system of balance relations obtained after Eq. (35) and Eq. (36) were integrated with initial conditions x(0) = x_i and t(0) = t_i:

Upon integrating Eq. (37), we receive an analytical expression for the moisture content of the material in the coordinates of the length of the rotating drum:

where

V(z) is the volume of the fluidized bed from the upload point to the coordinate z.

Unlike Eq. (37). Eq. (38) makes it possible to obtain an analytical solution only with the assumption that the heat capacity of the product remains average. If we agree that c = c_m + c_wu_am, where u_am is the average moisture content of the material, we obtain the following equation:

where dT/du = ν(dT/dτ).

By integrating Eq. (43) with the initial condition T(0) = T_i, we get:

where φ(u) = (u – u_e) / (u_i – u_e).

Formula (44) gives us values that are close to those we obtain after integrating Eq. (37), while the ratio error does not exceed 2.0%. This allows us to declare Eq. (43) and its analytical solution (44) applicable for analytical studies of continuous dehydration in a fluidized bed of bulk material.

Eqs. (37), (38), (40), and (41) make it possible to calculate the moisture content and the temperature of the dryable product in the fluidized bed along the length of the drying drum. We know the values of moisture content and coolant temperature only at the surface of the material. To calculate the parameters of the coolant at the outlet of the drying drum, we use the formulae for coolant mixing [11].

The equations for the moisture content and the temperature of the coolant at the outlet from the elementary volume of the fluidized bed (Fig. 9) can be formulated on the basis of Eqs. (31) and (32), if we assume that the temperature t_j and the moisture content x_j of the coolant at the outlet from the elemental volume are constant, and the coolant rate through this elementary volume is the difference in rates dL_j = L_j+1 – L_j, where L_j is the coolant rate when it is supplied to the fluidized bed in the section [0, z_j]:

where

The values of moisture content and the temperature of the coolant at the outlet of the drying chamber are calculated from the parameter values of the coolant flows that are coming out of all the elementary volumes of the fluidized bed, according to using the mix formulae of the flows:

If we use Eq. (42) and take into account that the kinetics of continuous drying is described by Eq. (27), while the flow of the bulk material moving on the cylindrical surface is presented as an ideal extrusion model (25), we can determine the equation of the effective continuous drying coefficient:

Relation (50) differs from others that determine the coefficient of drying. It is based on the analysis of the mechanics of a fluidized bed of wet solids on a cylindrical surface with regard to the continuous dehydration.

The model of the technical and economic characteristics. To assess the energy performance of a drying unit with the convective method of heat supply, one can assess the use of the drying agent. The energy losses are determined by the difference between the amount of the supplied and the usable energy [11, 12–15].

Various coefficients of efficiency are used as energy criteria. In the general case, they are defined as the ratio of the usable energy E₁ to the expended energy E₂:

For a convective drying process, the energy efficiency can be expressed by the following relation:

The thermoeconomic analysis combines exergy analysis and economic optimization. The criterion for the thermoelectric optimization is a composition of additive functions. These functions should quantify the exergy, the equipment costs, etc.

The most general formula for the so-called thermoelectric criterion is

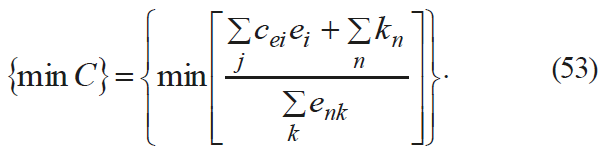
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

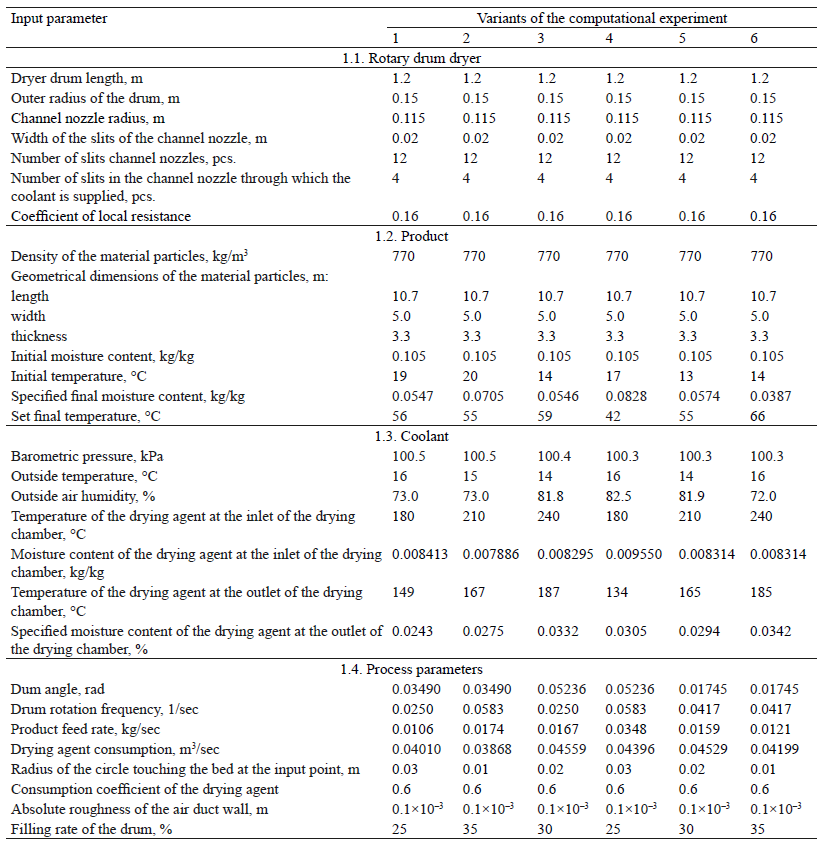
The research was based on the informational and structural scheme of a convective drying unit model. For all its components, we developed the mathematical models in accordance with the analytical multimodel system for the continuous drying process of wet solids in a fluidized layer. As a result, we constructed an automated calculation system for the continuous process of convective drying, which can be applied to a rotary drum dryer (Tables 1 and 2).

The practical result of the study consisted in assessing and comparing the quality indicators of sunflower seeds of natural moisture. First, one sample of sunflower seeds was dried on an experimental drum dryer with a channel nozzle. Second, another sample was dried on an industrial drum dryer with a lifting vane system at the vegetable oil plant ZAO ZRM Bobrovsky. Finally, the experimentally obtained results were compared with the computed results obtained from the mathematical model.

The experimental data show (Table 3) that after the sunflower seeds were dried in a drum dryer with a channel nozzle, the difference between the maximum and minimum humidity of individual seeds decreased by 2.34 times. This can be explained by the same residence time in the drying zone and the uniform distribution of the coolant flow in the fluidized bed.

The effect of the drying mode on the change in the quality of oil in the sunflower seeds (Table 4) was measured by changing the acid, peroxide, and iodine numbers at a different initial seed moisture. The heating temperature did not exceed the maximum permissible temperature for the particular humidity. It ensured the inactivation of enzymes, i.e. lipase and lipoxygenase.

Table 4 shows that the acid values of the oils in the studied modes were somewhat reduced. This can be explained by the fact that low molecular organic acids were distilled together with the water steam during the drying process. The peroxide numbers somewhat increased with increasing temperature, which can be explained by the catalytic effect of temperature on fat oxidation due to the presence of oxygen in the air. The iodine numbers decreased with increasing temperature. This resulted from the chemical reactions of breaking double bonds in the carbon chain of the fats and the addition of organic compounds and radicals that were present in the air.

Table 5 features some results of the comparative production tests. They confirm the fact that the temperature of the drying agent destroys protein structure. The number of damaged sunflower seeds when dried in a dense ventilated bed of moving seeds is significantly lower than in the fluidized bed.

The analysis of the physicochemical parameters of the oil suggests that the structure of the drying agent largely determined the quality of the dried sunflower seeds: acid, peroxide, and iodine numbers decreased by 12, 24, and 9% respectively.

If we compare the data obtained from the practical tests and from the model (Table 1), we can conclude that the results are reproducible. The following optimal values were also obtained while solving the problem of convective drying optimization: the initial moisture content of sunflower seeds was 16–17%; the temperature of the drying agent in the bed was 66–67%; the consumption of drying agent was (3.2–3.4)×10^–2 m³/sec; the angle of the drum was 0.61–0.70 rad; the drum rotation frequency was 3.6–4.2 min. These results agreed with the data of the model presented in Table 2.

ВЫВОДЫ

The proposed multimodel system of non-stationary drying processes for bulk materials has a number of advantages. First, it leads to a block-modular construction and expedient aggregation of rotary drum dryers. Second, it optimizes the allowances on the inputs and outputs of technological operations and links them together. Third, it develops requirements for the quality of raw materials and environmental conditions, in terms of the high efficiency of the organization of its processing.

Thus, when studying the specifics of heat transfer between the coolant and the solid particles of bulk material in a rotary drum dryer, most researches determine the average values of heat transfer coefficients. The proposed approach for calculating the effective heat transfer coefficient in a fluidized bed provides the required reproducibility and differs from the experimental data by no more than 2.0% (Table 2).

The energy performance of rotary drum dryers with a convective method of heat supply can be assessed according to the degree of the coolant use. The energy losses are determined by the difference between the amount of supplied and usable energy. It is more difficult to determine the optimal variant if it is necessary to satisfy several efficiency conditions. In this case, one should use compromise criteria, e.g. capital and energy costs, capacity, quality of the finished product, reliability of the management system, level of environmental safety, etc.

Nomenclature
τ – residence time of the bulk material in the dryer drum, sec;
G – dryer capacity, kg/sec;
ρ_db – dry bulk density, kg/msup>3;
V_d – dryer volume, m³;
G₁ – amount of material in the drum, kg;
G₂ – the amount of the material leaving the drum per unit of time, kg/sec;
V_m – volume of material unloaded from the drum, m³;
x₁(τ), x₁(τ) – the moisture content of the product and the coolant, respectively, kg/kg;
K – drying ratio, 1/sec;
G – consumption of the dryable product, kg/sec;
U(τ), L(z) – coolant flow rate, kg/sec;
q – moving mass flow, kg/sec;
ρ – density of the dryable product, kg/m³;
u – material speed, m/sec;
S – section area of the fluidized bed, m²;
a, b – constants determined experimentally;
u_e – equilibrium moisture content of the material, kg/kg;
T – product temperature, °C;
α – heat transfer coefficient, kW/(m₂×K);
t – coolant temperature, °C;
S_s – specific surface area of the material, m²/kg;
r – specific heat of vaporization, J/kg;
c_m, c_w – specific heat capacity of dry material and water, kJ/(kg×K);
S_p – surface of the particle, m²;
V_p – volume of the particle, m³;
ε – porosity of the fluidized bed;
V_s – specific volume of the coolant, m³/kg;
x(z) – moisture content of the coolant, kg/kg;
V_f – the volume of the fluidized bed of the bulk material in the rotating drum, m³;
ρ(u_e), ρ(u_i), ρ(u_f) – product density corresponding to the equilibrium, initial, and final moisture content of the material, kg/m³;
Nu_ORe, Nu_OAr – Nusselt numbers for forced and free movement forms, respectively;
c, m, n – constants of the equation;
n – drum speed per minute, min^-1;
φ – drum angle, rad;
ψ – the angle between the surface of the bed and the axis of the drum, rad;
Θ – friction angle of the material, rad;
R – the radius of the channel nozzle of the drum, m;
r₀ – the radius of the circle touching the bed at the input, m;
A – coefficient that takes into account the effect of the average flow rate in the bed of the wet solids on the throughput of the dryer, A = f(Re) is determined experimentally;
ξ – tortuosity coefficient of the channel;
w – flow rate in the direction of filtration, m/sec;
ρ_d, ρ_p – bulk density and particle density, kg/m³;
λ_g – the resistance coefficient of the granular bed;
w_w – flow rate in the direction of filtration, m/sec;
h – thickness of the bed, m;
ρ – density of the drying agent, kg/m³;
t₁, t₂, t₀ – temperature of the drying agent at the inlet and the outlet from the drying chamber and the temperature of the outside air, °C,
C – unit exergy value;
e_i – energy of the consumed raw materials and exergy;
c_ei – unit cost of exergy of the raw materials and energy;
e_nk – exergy of the products;
k_n – capital and other associated expenditures for the n-subsystem.

КОНФЛИКТ ИНТЕРЕСОВ

The authors declare that there are no conflicts of interest related to this article.

ФИНАНСИРОВАНИЕ

The research was conducted by the authors as a part of their work at the Voronezh State University of Engineering Technologies and ZRM Bobrovsky vegetable oil plant.

СПИСОК ЛИТЕРАТУРЫ

1. Antipov S.T., Panfilov V.A., Urakov O.A., and Shakhov S.V. Sistemnoe razvitie tekhniki pishchevykh tekhnologiy[Systemic development of food technology]. Moscow: KolosS Publ., 2010. 762 p. (In Russ.).
2. Zueva G.A., Kokurina G.N., Padokhin V.A., and Zuev N.A. Issledovanie teplomassobmena v protsesse konvektivnoy sushki voloknistykh materialov [A research on heat and mass transfer in the process of convective drying of fibrous materials]. Russian Journal of Chemistry and Chemical Technology, 2010, vol. 53, no. 7, pp. 93–96. (In Russ.).
3. Akulich P.V., Temruk A.V., and Akulich A.V. Modeling and experimental investigation of the heat and moisture transfer in the process of microwave-convective drying of vegetable materials. Journal of Engineering Physics and Thermophysics, 2012, vol. 85, no. 5, pp. 951–958. (In Russ.).
4. Frolov V.F. Macrokinetic analysis of the drying of particulate materials. Theoretical Foundations of Chemical Engi- neering, 2004, vol. 38, no. 2, pp. 133–139. (In Russ.).
5. Bon J. and Kudra T. Enthalpy – Driven Optimization of Intermittent Drying. Drying Technology, 2007, vol. 25, no. 4, pp. 523–532. DOI: https://doi.org/10.1080/07373930701226880.
6. Vaquiro H.A., Clemente G., Garcia-Perez J.V., Mulet A., and Bond J. Enthalpy-driven optimization of intermit- tent drying of Mangifera indica L. Chemical Engineering Research and Design, 2009, vol. 87, no. 7, pp. 885–898. DOI: https://doi.org/10.1016/j.cherd.2008.12.002.
7. Glouannec P., Salagnac P., Guézenoc H., and Allanic N. Experimental study of infrared-convective drying of hy- drous ferrous sulphate. Powder Technology, 2008, vol. 187, no. 3, pp. 280–288. DOI: https://doi.org/10.1016/j. powtec.2008.03.007.
8. Antipov S.T., Zhuravlev A.V., Kazartsev D.A., et al. Innovatsionnoe razvitie tekhniki pishchevykh tekhnologiy [Inno- vative development of food technology techniques]. St. Petersburg: Lan Publ., 2016. 660 p. (In Russ.).
9. Sazhin B.S., Otrubjannikov E.V., Kochetov L.M., and Sazhin V.B. Drying in active hydrodynamic regimes. Theoreti- cal Foundations of Chemical Engineering, 2008, vol. 42, no. 6, pp. 638–653. (In Russ.).
10. Padokhin V.A., Zueva G.A., Kokurina G.N., Kochkina N.E., and Fedosov S.V. Complex Mathematical Description of Heat and Mass Transfer in the Drying of an Infinite Cylindrical Body with Analytical Methods of Heat-Conduction Theory. Theoretical Foundations of Chemical Engineering, 2015, vol. 49, no. 1, pp. 54. (In Russ.)
11. Bobkov V.I. Issledovanie tekhnologicheskikh i teplo-massoobmennykh protsessov v plotnom sloe dispersnogo ma- teriala [A research on technological and heat and mass transfer processes in a dense layer of dispersed material]. Thermal Processes in Engineering, 2014, no. 3, pp. 139–144. (In Russ.).
12. Ol’shanskii A.I. Study of the heat transfer in the process of drying of moist materials from experimental data on moisture transfer. Journal of Engineering Physics and Thermophysics, 2014, vol. 87, no. 4, pp. 887–897. (In Russ.).
13. Ol’shanskii A.I. Heat transfer kinetics and experimental methods for calculating the material temperature in the drying process. Journal of Engineering Physics and Thermophysics, 2013, vol. 86, no. 3, pp. 584–594. (In Russ.).
14. Chin S.K. and Law C.L. Product quality and drying characteristics of intermittent heat pump drying of Ganoderma tsugae Murrill. Drying Technology, 2010, vol. 28, no. 12, pp. 1457–1465. DOI: https://doi.org/10.1080/07373937.20 10.482707.
15. Sokolowskyy Ya., Dendiuk M., and Bakaletz A. Mathematical modeling of the two-dimensional moistural and visco- elasticity states of wood in the process of drying. IAWS plenary meeting and conference “Forest as renewable source of vital values for changing world”. St. Petersburg – Moscow, 2009, p. 120.