Аннотация

The article summarizes some scientific and practical prerequisites for creating multicomponent foods with desirable quality characteristics and consumer properties. Mathematical methods were used to model a multicomponent product according to the selected parameters of adequacy and quality, depending on the nutritional and biological value of raw materials. The Russian methodology of food design originated in the works of N.N. Lipatov. His six basic principles of designing balanced multicomponent foods are still relevant today. Further development was proposed by A.B. Lisitsyn who took into account individual protein digestibility of every component in the mixture and its effect on the amino acid composition of total protein. At the next stage, Yu.A. Ivashkin improved formulations using the methods of system analysis, modelling, and product range optimization. Modern food chemistry, food biotechnology, and information technologies allow for effective computer design and optimization of multicomponent food formulations for specific population groups. As a result, an increasing number of food scientists are engaged in improving food products. Literature analysis showed that the current stages of designing (modelling) multicomponent foods are mainly based on information and algorithms, using linear, experimental and statistical programming methods or an object-oriented approach. Russian food scientists still use the methodology developed by A.M. Brazhnikov, I.A. Rogov, and N.N. Lipatov. It allows for designing multicomponent foods with specified nutritional indicators and energy value. The Russian Academy of Sciences pointed to a need for “digital nutritiology” (Decree No. 178 of November 27, 2018 “On Current Problems of Optimizing the Population of Russia: Role of Science”). This new scientific direction could enable digital transformation of data on human physiological needs for nutrients, biologically active substances, and energy, as well as the chemical composition of basic foods. There is also a need for computer programs to give personalized recommendations for optimal nutrition.

Ключевые слова

Design, multicomponent products, criteria, optimization

ВВЕДЕНИЕ

In designing multicomponentI food products, of great importance is an opportunity to model characteristics of the finished product and predict its quality, as well as functional and technological properties [1, 2].

Designing multicomponent products is based on the principle of food combinatorics. This process involves creating new formulations through a careful selection of raw materials, ingredients, as well as dietary and biologically active additives. Such combinations make the product balanced and ensure the required sensory and physicochemical properties, as well as nutritional, biological, and energy values [3, 4].

The information base created by many years of Russian scientific efforts is highly instrumental in improving food formulations through the use of design criteria and concepts.

This article offers a review of some theoretical and practical results achieved by the Russian science of “food combinatorics” from its foundation to the present day.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

A.M. Brazhnikov and I.A. Rogov were the first Soviet scientists who formulated the principles for mathematical design of multicomponent foods with a required set of consumer properties [5, 6].

Back then, food design meant developing models to govern all stages of creating a product of required quality. At the same time, it prioritized a need to express quality in quantitative terms.

A.M. Brazhnikov et al. classified food products into three groups to develop the analytical method [5]. Group I included those products (porridge, curd cheese, paste) whose components were interchangeable, both in terms of their relation to each other and their position in the general system. The relationships between the components were not taken into account. To describe the properties of those products, the authors used the general principles of thermodynamics.

Group II covered those products (minced meats, sausages, bread, butter, vegetable pastes, etc.) whose components could interact with each other in various ways without having a fixed position in the system. Their distinctive feature was that the physicochemical interaction of their components during processing could have highly significant effects on the quality of the finished product. The principle of superposition could not be applied to Group II in the same way as it could be applied to Group I. Thus, the authors concluded that designing Group II products required a greater awareness of the product characteristics and a quantitative expression of relationships between the components.

Finally, Group III included products (cakes, ready-toeat foods, etc.) with interchangeable components and a rigidly fixed structure.

Thus, the authors set out the initial provisions of the analytical approach to designing meat products [5]. This approach was further developed by creating methods to determine specific quality indicators.

In 1980–1990, the most developed methods were those for designing binary systems. It was difficult to achieve a specific amino acid profile in the protein systems of three or more components. In 1980, V.A. Shaternikov proposed the first analytical approach to designing food products with a binary composition [7].

The mass fraction of any j-th amino acid in the binary composition was calculated as:

where A_j is the content of the j-th essential amino acid, g/100 g protein;
A_1j and A_2j are the contents of the essential amino acid in the first and second components, g/100 g protein;
X₁ and X₂ are mass fractions of the first and second type proteins in the binary system (X₁ + X₂ = 1).

The scores of the m-th and n-th essential amino acids (used to optimize the binary composition) were calculated as:

where X₁, X₂ are mass fractions of the first and second type proteins in the binary system (X₁ + X₂ = 1);
A_1j and A_2j are mass fractions of the j-th amino acid (including the n-th and m-th essential amino acids) in the first and second type proteins, g/100 g protein;
F_m and F_n are mass fractions of the m-th and n-th essential amino acids in the reference protein, g/100 g protein.

Below are proposed solutions for three typical situations.

First situation. If both proteins have a limited content of the same essential amino acid (given C_m = C_n), the composition protein score is a constant value equal to C_m = C_n, regardless of X₁ and X₂.

Second situation. If the first protein has a limited content of the m-th essential amino acid, while the second protein has it in excess (compared to the reference protein), the optimal ratio of X₁ and X₂ is determined by solving a system of linear equations:

Another condition is needed for system (3) to determine the optimal ratio of X₁ and X₂, namely: A_1n ≥ F_n and A_2n ≥ F_n.

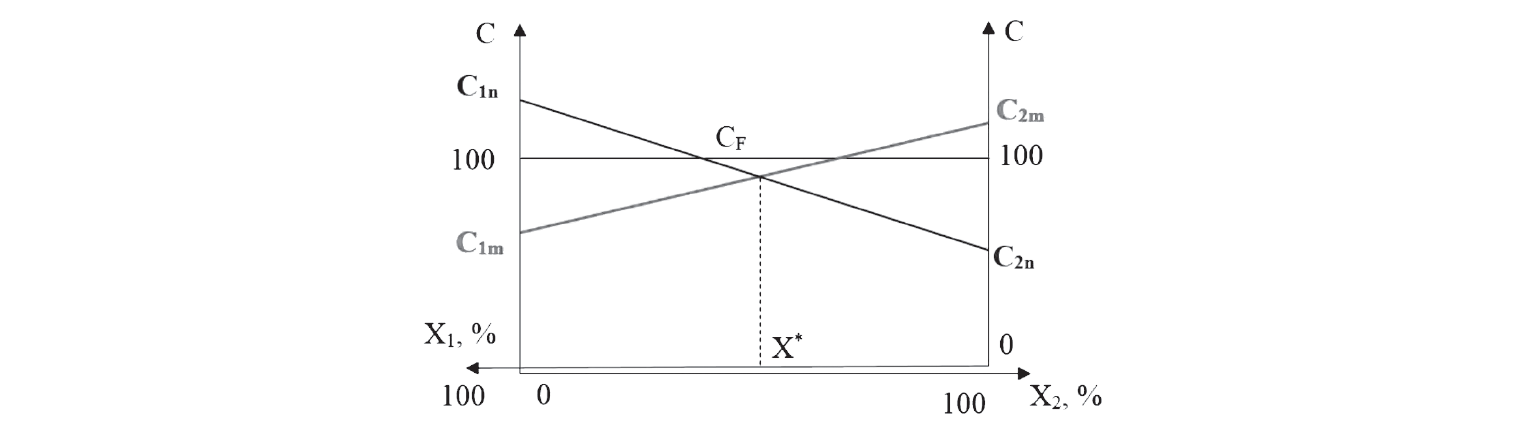
Third situation. If the first component has a limited content of the m-th amino acid and an excessive content of the n-th amino acid (A_1n > F_n; A_1m < F_m), while the second component has a limited content of the n-th amino acid and an excessive content of the m-th amino acid (A_2m > F_m; A_2n < F_n), the optimal ratio between X₁ and X₂ in the binary system is determined by the graphical method (Fig. 1). This method allows a quick determination of the required values that ensure the maximum score of the limiting amino acid in the composition.

In 1983, this approach was approved by the USSR Ministry of Health within Guidelines No. 2688-83 for using milk and soy proteins in meat production.

In 1981, N.A. Mikhailov (whose research supervisors were I.A. Rogov, Doctor of Technical Sciences and V.G. Vysotsky, Doctor of Medicine) developed some basic analytical principles of designing combined products based on modelling the biological value of protein. He used those principles to create combined paste, as well as a number of cereals and diabetic protein-wheat bread with an increased biological value [8–12].

In addition, N.A. Mikhailov proposed a comprehensive statistical model of protein biological value to determine the optimal composition of ingredients in combined products or correct the initial ratio of ingredients to ensure a specific biological value after heat treatment.

N.N. Lipatov (Jr.) proposed a completely different classification of food products that is still used today for designing functional products [13–16]. In particular, it includes three generations of industrial foods:

‒ products that have sensory characteristics similar to traditional ones, with raw materials partially replaced with hydrated components equivalent in protein content;
‒ multicomponent products with a nutrient ratio close to a statistically sound standard that take into account the metabolism in specific population groups united by nationality, age or other characteristics; and
‒ products with a specially selected combination of components that can ensure their targeted use as functional products by certain population groups.

In addition, N.N. Lipatov developed six basic principles for formulating balanced foods and diets [13–16], namely:

‒ compliance with a rationally balanced formulation;
‒ compliance of an amino acid composition of proteincontaining ingredients with a statistically sound reference protein;
‒ a possibility of changing the fatty acid composition by adding fat-containing ingredients;
‒ the nearest approximation to a desirable ratio of saturated, monounsaturated, and polyunsaturated fatty acids in any combination of fat-containing ingredients;
‒ taking into account the composition of other dishes and foods in the diet; and
‒ a balanced multicomponent composition for a single or daily ration in terms of energy value, macro- and micronutrients, and ballast agents.

These principles are still used as a foundation for research in the field of food combinatorics.

N.N. Lipatov et al. conducted several studies to develop methods for creating foods with a specified nutritional value [13–16]. In doing so, they assumed that the mechanical processing of raw materials to ensure the required level of dispersion or structural and mechanical characteristics did not violate the principle of superposition with respect to their biologically valuable nutrients. They used this hypothesis in making logical constructions about deterministic formalized approaches to measuring the quantity of individual ingredients. As a result, the authors made valid and reliable conclusions about formulating products with a specified nutritional value and formalized the qualitative and quantitative conceptions about the rationality of using essential amino acids in the technology of adequate exotrophy. Formalization takes into account the mutual balance of essential amino acids.

The scientists formulated the main principle and criterion for the rational use of essential amino acids in new types of foods. The principle gives preference to such combinations of n-protein-containing components withmass fractions X_i^p in which the maximum proportion of assimilable essential amino acids in the protein, given equal provision of the body with anabolic material, can be used for anabolic purposes without degradation in the biosynthesis of nonessential amino acids, let alone biological oxidation in compensating for the energy expenditure of the body [13].

Taking into account a possibility of C_min ≥1 min (where C_min is the minimum score of essential amino acids in the protein of the designed product in relation to the reference protein) or a possibility of C_min <1, the selection criterion X_i^p can be symbolically presented as

where A_α^∑ is the total mass fraction of assimilated essential amino acids that can be used by the body for anabolic purposes without further degradation;
A_φ^∑ is the actual sum of assimilated essential amino acids.

The authors transformed the above formula introducing p_i as a mass fraction of digestible protein in the i-th component (%) and a_ij as a mass fraction of the ј-th essential amino acid in the protein of the i-th component (g/100 g). Criterion (4) for finding a preferable ratio of the mass fractions X_i^p of these components in the designed product with regard to rational use of the k essential amino acids can be presented as:

where

is the mass fraction of j-th essential amino acid in protein of the designed products with the fixed j, g/100 g protein;
A_rj is the reference mass fraction of the j-th essential amino acid, g/100 g protein.

N.N. Lipatov (Jr.) developed the following methodological approaches to designing foods with the required set of nutritional indicators.

The first stage involves modelling the amino acid composition of protein in the designed product and selecting X_i^p that provide the minimum functional value (4).

The second stage involves modelling the fatty acid composition, given that the mass fractions of components X_i containing protein, as well as fat, are constant and predetermined by the first stage. Based on the modelling results, mass fractions X_i are selected that together with X_i provide the required approximation to the physiologically determined ratio of saturated, monoand polyunsaturated fatty acids.

The third stage involves calculating the energy value Q_p of the designed product, taking into account only those X_i^c(p,L) which are sources of protein and/or fat. The result is then compared with the required Q. If the estimated energy value is less than Q, the product is supplemented with additional technologically permissible carbohydrate-containing components in quantities that ensure the required Q. If Q_p is greater than Q, X_i^L are recalculated. If necessary, X_i^L with excessively high L_i values can be replaced with those with lower L_i values.

Using the Mitchell-Block principle, N.N. Lipatov developed a number of indicators, namely: the utilization coefficient for essential amino acids; the utilization coefficient for the amino acid composition of the product, g/100 g protein; the ratio of amino acids as a balance of essential amino acids in relation to the physiologically determined norm (standard); and the indicator of excess in the content of essential amino acids as the total amount of essential amino acids that are not used for anabolic purposes [17, 18].

Thus, we can conclude that the main studies of N.N. Lipatov were devoted to the trophological, mathematical, informational, and algorithmic aspects of food design. He supervised the creation of ordinary and specialised products for baby and gerodietetic nutrition. Finally, he established a scientific school to improve the quality of foods considered as objects of a single exotrophic chain of production, consumption, and assimilation of nutrients by the human body.

A.B. Lisitsyn combined the mathematical methods of I.A. Rogov and N.N. Lipatov for calculating the amino acid composition and total protein digestibility in multicomponent mixtures [19–21].

Protein digestibility is one of the most important indicators of the product’s biological value, along with its amino acid balance. A.B. Lisitsyn understood the need to take into account individual protein digestibility of all components when estimating the product’s biological value and study their effect on the amino acid composition of total protein. The mathematical interpretation of his concept can be presented as follows:

where A_j is the content of j-th amino acid, g/100 g protein;
X_i is the mass fraction of the i-th component in the mixture, unit fraction;
π_i is the dimensionless characteristic (coefficient) of protein digestibility of the i-th component;
p_i is the mass fraction of protein in the i-th component, % or unit fraction;
a_ij is the mass fraction of j-th amino acid in the protein of the i-th component, g/100 g protein;
n is the total number of ingredients in the formulation;
(n-m) is the number of replacement ingredients during modelling;
L is the number of ingredients that are not replaced during modelling;
(m-L) is the number of ingredients varying (replaced) during modelling;
Y is the total amount of varying ingredients in the formulation.

Thus, A.B. Lisitsyn substantiated the principles of designing meat products with a given biological value, taking into account individual protein digestibility and the amino acid composition of every ingredient in the formulation. His mathematical formulas allow us to devise the amino acid composition of multicomponent systems, taking into account individual protein digestibility of every component.

Yu.A. Ivashkin combined the structural and the parametric optimization approaches in his works. Structural optimization is the determination of optimal structural parameters of the formulation. Parametric optimization involves calculating optimal deviations from the norm. Yu.A. Ivashkin et al. suggested using structural and parametric optimization for every criterion with pairwise comparison and quality assessment of the resulting product using an independent quality functional and desirability scales [22, 23]. The multicriteria optimization of the combined product (nutritional and biological values) consists in building its model according to the specified adequacy and quality parameters, depending on the composition of initial components.

For this, a parametric model of the product is devised, taking into account:

– the required chemical composition (protein, fat, carbohydrates, etc.);
– mass fractions of the main components (key ingredients, fiber, biologically active additives, enzymes, etc.); and
– structural relationships of biological value indicators (amino and fatty acid compositions) according to various compliance criteria.

Consideration is also given to what makes a balanced diet for a certain population group.

An objective function is the minimum diviation from the given structural group of nutritional and biological indicators [22, 23], namely the criteria below.

(1) The optimization criterion for chemical elements that determine the nutritional value P(z) of the designed product:

where z_i⁰ is the reference content of the i-th element of nutritional value;
b_ij is the specific content of the i-th element of chemical composition in the j-th component of the designed product;
x_j is the mass fraction of the j-th component.

(2) The criterion of the minimum deviation from the given structural indicators of biological value P_i(A), for example, the monostructure of essential amino acids (i = 1) and fatty acids (i = 2):

where A_k⁰ is the reference content of the k-th monostructural indicator of biological value;
a_ki is the specific content of the k-homonostructural ingredient in the i-th element of chemical composition;
b_ij is the specific content of the i-th element of chemical composition in the j-th component of the designed product;
x_j is the mass fraction of the j-th component.

(3) The criterion of the minimum deviation from the given structure P_i(V) of the vitamin composition (i = 1), minerals (i = 2), and carbohydrates (i = 3):

where b_kj is the specific content of the k-th ingredient in the j-th element of chemical composition;
x_j is the mass fraction of the j-th component.

Yu.A. Ivashkin proposed to use simulation modelling to solve the problem of structural and parametric optimization of a multicomponent product in various combinations of linear and non-linear criteria and restrictions. It involves “playing out” all possible combinations of initial ingredients with subsequent verification of restrictions and calculation of criteria.

Noteworthily, any problem of the NP class can be solved by simulation modelling. The complexity depends on the number of ingredients in the formulation. If the space of problem solutions is very large, this method may take longer than a “reasonable” time to produce results.

A.E. Krasnov et al. used new information technologies to produce foods of given quality. In particular, they created sausage meat formulations under varying conditions of uncertainty. Their study showed how to transform the problem of stochastic programming with uncertain target criteria into the linear programming problem with stochastic constraints [24].

Considerable attention is now paid to modelling interactions between food components based on the laws of equilibrium statistical thermodynamics. For the first time, a polynomial dependence was found between the properties of food mixtures and the mass fractions of their ingredients. Its relationship with macroscopic thermodynamic parameters of the mixtures was also shown.

Scientific modelling of multi-component food products with a specific set of nutritional and energy indicators is still relevant worldwide. An ever wider circle of researchers are engaged in various aspects of improving food technology.

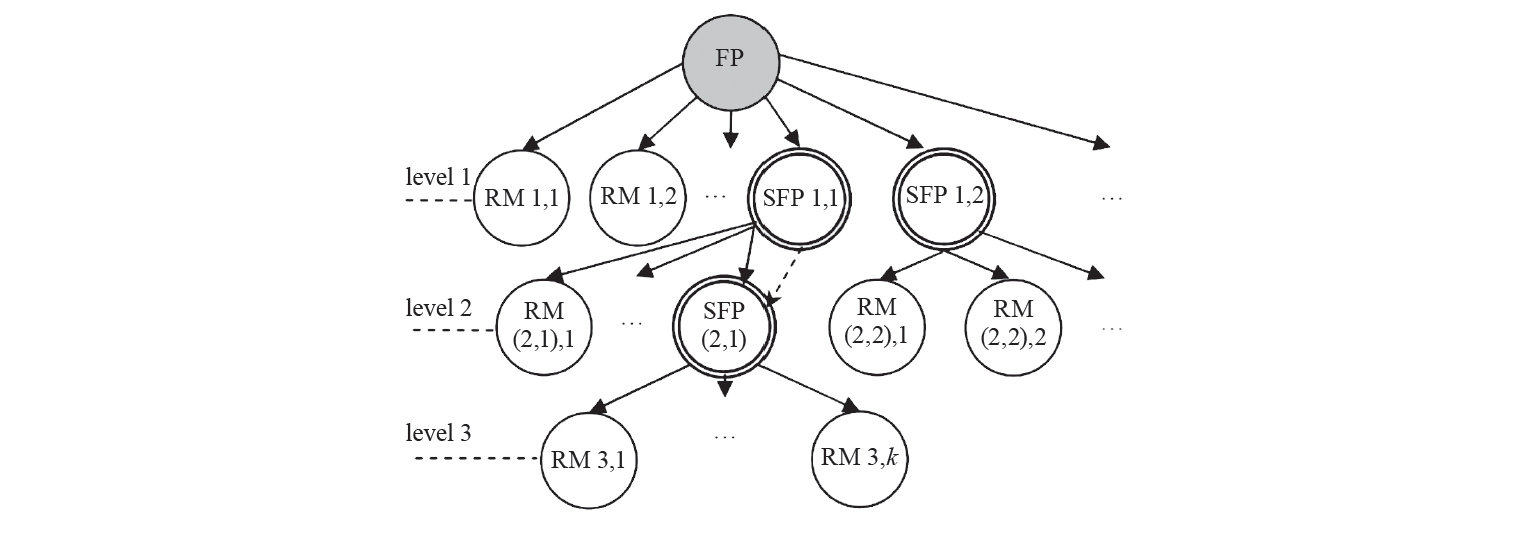
E.I. Muratova et al. proposed an object-oriented approach to designing multicomponent food products (for example, confectionery). A distinctive feature of this approach is presenting a formulation as a hierarchical structure (the Saati method) [25, 26].

Each vertex of this structure is an object (raw materials – semi-finished product – finished product). Each level is a certain stage of food technology that can have its own number of vertices located lower in the hierarchy. The algorithm for calculating a multicomponent product begins with the lowest level in the longest branch of the hierarchical structure (Fig. 2).

Figure 2 shows a three-level hierarchy of formulation, where the first index is the level number and the second is the number of a component in the formulated mixture. When several semi-finished products are used at the same level, their first index becomes a composite and is indicated as a list (i, j), where i is the level number and j is the serial number of the semi-finished product at the i-th level. This composite index is used lower in the hierarchy (shown by the dashed arrow).

The algorithm for calculating the multiphase formulation begins with the lowest level in the longest branch of the hierarchical structure. According to Fig. 2, the calculation of the formulation begins with the semi-finished product FP (2, 1), since the path to its components is the longest in the hierarchy. The initial data for calculating the lowest level include the loading of all types of raw materials and semi-finished products, loss of dry matte, and a given amount of finished products equal to 1 t.

According to the authors, the main advantage of this approach is the object-oriented representation. It allows for inheriting properties and methods while adding new calculation formulas that take into account new raw materials, production features, as well as technical and economic indicators of the processes.

O.N. Musina and P.A. Lisin proposed a methodology for system modelling of multicomponent food products [27–29]. They defined system modelling as a strategy for studying and creating biosystems, particularly food products, their formulations, and production technologies.

The basic principle of system modelling is the decomposition of a complex biosystem into simpler subsystems. This is a principle of the system hierarchy. In this case, the mathematical model of the system is based on the block principle: the general model is divided into blocks which can have relatively simple mathematical descriptions. All subsystems interact with each other and constitute a common unified mathematical model.

Figure 3 shows a visual interpretation of the basic principles of system modelling of multicomponent products.

System modelling principles allow for the decomposition of the production system at the stage of formulating composite mixtures using linear models. In such models, mathematical dependencies (equalities or inequalities) are linear with respect to all variables in the model. Problems of this kind are used to select the optimal option from a set of possible formulations according to a given criterion. In 1939, the Russian mathematician L. Kantorovich and the American scientist G. Danzig began to develop what was later called “the simplex metho”. It became a universal method of linear programming used in solving optimization problems.

A.A. Borisenko proposed a methodology for optimizing multicomponent food mixtures using universal mathematical methods. His methodology allows for the development of foods with a given nutrient composition [30, 31]. Taking into account certain restrictions and permissible deviations of nutrient mass fractions from the reference amounts, the author proposed to use the Lagrange function and the system of equations in the form of conditions of the Kuhn-Tucker theorem for convex programming. Solving these problems produces a vector of component mass fractions to ensure the most balanced nutrient composition.

The author concluded that the most balanced formulation cannot always guarantee the highest quality of the finished product. Therefore, in most cases, there is a need for a fairly wide range of formulated options. To achieve that, he proposed to optimize formulations in two stages. The first stage of modelling a formulation involved determining all possible quantitative ratios of the ingredients. The second stage was a qualitative assessment and selection of several most optimal variants. The author used Harrington’s desirability function as a general criterion for quality assessment.

A.Yu. Prosekov developed the principles of forming dispersed food systems and designing functional products from modern perspectives [32–34].

T.V. Sanina and Yu.S. Serbulov proposed a differentiated approach to a comprehensive assessment of highly nutritional bakery products. The authors believe that consumers should select key quality indicators for foods with increased nutritional value to make their assessment objective. In addition, quality assessment should check if the product satisfies certain needs consistent with its purpose [35].

A.A. Zaporozhsky et al. formulated new gerodietetic products with specified qualitative characteristics based on natural raw materials. For this, they used a methodological approach and the principles of modern nutrition, qualimetry, food combinatorics, and neural network approximation of theoretical (estimated) and experimental data [36, 37].

T.Yu. Reznichenko et al. substantiated an integrated technological approach to the development of functional foods enriched with biologically active substances and dietary fibre. They studied the factors that determine the quality of specialized products and critical control points that identify their functional character at the stages of production and distribution. They also developed a range of consumer properties that included functional indicators in addition to sensory and physicochemical characteristics. Finally, the authors developed an algorithm to examine a functional cereal breakfast bar [38, 39].

V.M. Kiselev and E.G. Pershina looked at the production and consumption of functional foods as a multi-factor system subjected to comprehensive assessment. They used the methods of food combinatorics, parity of needs, and the vital concept, taking into account modern requirements of nutrition. With this approach, the authors studied a possibility of evolutionary development of functional food design based on food combinatorics. They identified consumer preferences for functional foods and systematized them in a model of consumer value [40].

O.N. Krasulya et al. considered the design of multicomponent foods based on the functional and technological properties (FTP) of their main raw materials and ingredients. They also took into account the kinetics of biochemical and colloidal processes, as well as analytical and empirical relations characterizing the main patterns of heterogeneous disperse systems with varying physicochemical factors [42, 43].

In the age of digital (information) technologies, the design of multicomponent food formulations can be improved by using linear, experimental and statistical programming methods, or an object-oriented approach. M.S. Koneva et al. proposed using neural network technologies [44]. The relationship between sensory criteria and the quantitative composition of the formulation was identified by neural network and regression analysis of the ranking score of sensory characteristics. The model parameters were obtained with Statistica software. The convolution of the balancing index and sensory evaluation was proposed as a multiplicative desirability function. MathCAD scripts were used to optimize the composition of antianemic smoothie for pregnant women.

N.A. Berezina et al. developed a program in Object Pascal for designing gerodietetic bread compositions [45]. The technological adequacy of the flour mix, which ensured a stable quality of the final product, was modelled by introducing the flour technological indicator (“falling number”) calculated using the Perten formula.

The mathematical foundations of solving singlecriterion optimization problems are quite well studied today. However, various areas of engineering, research and management have multicriteria problems in which several criteria need to be simultaneously optimized. M.A. Nikitina and I.M. Chernukha proposed using the Pareto method for multicriteria optimization [46].

The informational aspects of modelling and evaluating the nutritional adequacy of raw materials and finished products are very important in improving the quality and technology of specialized multicomponent food products.

ВЫВОДЫ

The analysis of literature on the principles and methods of designing balanced foods showed that the initial stage in this process involved formalizing qualitative and quantitative assumptions about the rational use of essential amino acids in the adequate exotrophy technology. N.N. Lipatov’s contribution to designing balanced formulations in Russia cannot be underestimated. His principles of creating multicomponent foods and balanced diets are still relevant today. Further development of food combinatorics was related to informational and algorithmic aspects of food design.

The conceptual approaches to computer-aided food design proposed by N.N. Lipatov (Jr.) are used to model functional products with specified qualitative characteristics. Based on the optimal choice of raw materials and ratios of ingredients, they result in formulations whose nutrients (essential amino acids, unsaturated fatty acids, macro- and microelements, and vitamins) are consistent with the medical and biological requirements in terms of quantity and quality.

The computer systems and software products actively used in Russia to automate technological calculations for food and diet formulations include Etalon, Generic 2.0, Food & Life, CheesePro 1.0, ShkoOptiPit, and others. They are based on the databases of foods and raw materials, scientific research and industrial experience, as well as mathematical methods of modelling and designing food covered in the works of I.A. Rogov, A.M. Brazhnikov, N.N. Lipatov (Jr.), and other scientists. With the help of those systems, new types of products were developed by Moscow State University of Applied Biotechnology, Gorbatov All-Russia Meat Research Institute, Research Institute of Baby Food, All-Russia Research Institute of Dairy Industry, and other institutes. These products had an improved composition of chemical elements, amino and fatty acids, as well as better energy values, quality indicators, etc. The experimental and theoretical (mathematical) data were 98% reliable.

The foreign software solutions (DietPlan, Nutri-Survey, NutriBase, NUT, MyFitnesspal, and 8fit) are based on calculating the individual’s daily energy intake and their need for basic nutrients.

Designing foods in the digital age, we need to take into account not only nutritional and biological values, but also medical, technological, economic, social, and other factors. Computer technologies allow us to address problems with numerous parameters, alternatives, and criteria, as well as restrictions and conditions. By processing and formalizing data, they help us find optimal solutions based on complex optimization models and objective assessment of options.

A need for “digital nutritiology”, a new scientific field, was highlighted in Decree of the Presidium of the Russian Academy of Sciences No. 178 dated November 27, 2018 “On the Current Problems of Optimizing the Population of Russia: Role of Science” (paragraph 11). This new direction is supposed to translate into the language of numbers our physiological needs for energy, nutrients, biologically active substances, and balanced diets, on the one hand, and the chemical composition of foods and general diets, on the other.

КОНФЛИКТ ИНТЕРЕСОВ

The authors state that there is no conflict of interest.

ФИНАНСИРОВАНИЕ

This work was financially supported by the Russian Science Foundation, project No. 16-16-10073-P.

СПИСОК ЛИТЕРАТУРЫ

1. Lisitsyn AB, Nikitina MA, Zakharov AN, Sus EB, Nasonova VV, Lebedeva LI. Prediction of meat product quality by the mathematical programming methods. Theory and Practice of Meat Processing. 2016;1(1):75–90. (In Russ.). DOI: https://doi.org/10.21323/2114-441X-2016-1-75-90.
2. Prosekov A, Babich O, Kriger O, Ivanova S, Pavsky V, Sukhikh S, et al. Functional properties of the enzyme-modified protein from oat bran. Food Bioscience. 2018;24:46–49. DOI: https://doi.org/10.1016/j.fbio.2018.05.003.
3. Zharinov AI, Ivashkin YuA. Proektirovanie kombinirovannykh produktov pitaniya [Designing combined foods]. All about the meat. 2004;(2):16–21. (In Russ.).
4. Zharinov AI, Ivashkin YuA. Proektirovanie kombinirovannykh produktov pitaniya [Designing combined foods]. All about the meat. 2004;(3):6–15. (In Russ.).
5. Brazhnikov AM, Rogov IA. O vozmozhnosti proektirovaniya kombinirovannykh myasnykh produktov [On designing combined meat products]. Myasnaya industriya SSSR [Meat industry in the USSR]. 1984;(5):23–25.
6. Brazhnikov AM, Rogov IA, Mikhaylov NA, Silʹchenko MN. Vozmozhnye podkhody k analiticheskomu proektirovaniyu kombinirovannykh produktov pitaniya [Possible approaches to the analytical design of combined foods]. News institutes of higher education. Food technology. 1985;166(3):22–27. (In Russ.).
7. Shaternikov VA. Mediko-biologicheskie aspekty problemy obogashcheniya pishchevykh belkov [Biomedical aspects of the problem of enrichment of food proteins]. Teoreticheskie i klinicheskie aspekty nauki o pitanii: sbornik nauchnykh trudov. Tom 1 [Theoretical and clinical aspects of nutrition science: a collection of scientific papers. Vol. 1]; 1980. Moscow. Moscow: Institut pitaniya AMN USSR; 1980. pp. 134–160. (In Russ.).
8. Mikhaylov NA, Silʹchenko MN. Optimizatsiya s pomoshchʹyu EHVM summarnogo kolichestva nezamenimykh aminokislot pri chastichnoy zamene myasa belkovymi preparatami [Computer-aided optimization of total essential amino acids with partial replacement of meat with protein preparations]. Materialy Vsesoyuznoy nauchnotekhnicheskoy konferentsii “Tekhnologiya i tekhnika myasnoy i molochnoy promyshlennosti na osnove sovremennykh issledovaniyakh” [Proceedings of the all-union scientific and technical conference “Technology and equipment in the meat and dairy industries based on modern research”]; 1981. Moscow. Moscow, 1981. p. 13. (In Russ.).
9. Mikhaylov NA, Dynkin IV, Safronova AM, Gurʹyanov VA. Izuchenie optimalʹnogo sootnosheniya razlichnykh belkovykh dobavok, vvodimykh v myasoprodukty [Studying optimal ratios of various protein additives introduced into meat products]. Tezisy dokladov konferentsii molodykh spetsialistov [Abstracts from the conference of young researchers]; 1982; Moscow, 1982. pp. 137. (In Russ.).
10. Rogov IA, Mikhaylov NA, Statnykh SA, Kalugin SEh. Optimizatsiya aminokislotnogo sostava belkovykh smesey s pomoshchʹyu EHVM [Abstracts from the conference of young researchers]. News institutes of higher education. Food technology. 1982;147(5):153. (In Russ.).
11. Gurʹyanov VA, Mikhaylov NA, Statnykh SA, Silʹchenko MN. Matematicheskoe modelirovanie “idealʹnogo” belka [Mathematical modelling of the “ideal” protein]. Materialy I Vsesoyuznoy nauchno-tekhnicheskoy konferentsii “Razrabotka protsessov polucheniya kombinirovannykh myasoproduktov” [Proceedings of the 1st all-union scientific and technical conference “Developing production processes for combined meat products”]; 1982; Moscow, 1982. pp. 121–122. (In Russ.).
12. Mikhaylov NA, Silʹchenko MN. Nomogrammnyy metod opredeleniya biologicheskoy tsennosti mnogokomponentnykh belkovykh system [The nomogram method for determining the biological value of multicomponent protein systems]. Materialy II Vsesoyuznoy nauchno-tekhnicheskoy konferentsii “Razrabotka protsessov polucheniya kombinirovannykh produktov” [Proceedings of the 2nd all-union scientific and technical conference “Developing production processes for combined products”]; 1984; Moscow, 1984. pp. 89–90. (In Russ.).
13. Lipatov NN. Metody kolichestvennoy otsenki i modelirovaniya aminokislotnoy sbalansirovannosti produktov myasnoy promyshlennosti [Methods for quantifying and modelling the amino acid balance of meat products]. XXXI Evropeyskiy kongress nauchnykh rabotnikov myasnoy promyshlennosti [The 31st European congress of meat scientists]; 1985; Sofia. Sofia, 1985. pp. 158–161. (In Russ.).
14. Lipatov NN. Predposylki kompʹyuternogo proektirovaniya produktov pitaniya s zadavaemoy pishchevoy tsennostʹyu [Prerequisites for computer-aided design of foods with specified nutritional values]. Storage and Processing of Farm Products. 1995;(3):4–9. (In Russ.).
15. Lipatov NN, Sazhinov GYu, Bashkirov OI. Formalizovannyy analiz amino- i zhirnokislotnyy sbalansirovannosti syrʹya, perspektivnogo produktov detskogo pitaniya s zadavaemoy pishchevoy adekvatnostʹyu [Formalized analysis of amino and fatty acid balance of raw materials for baby foods with specified nutritional adequacy]. Storage and Processing of Farm Products. 2001;(8):11–14. (In Russ.).
16. Lipatov NN. Nekotorye aspekty modelirovaniya aminokislotnoy sbalansirovannosti pishchevykh produktov [Some aspects of modelling the amino acid balance of foods. Food and processing industry]. Food and processing industry. Abstract journal. 1986;(4):48–52. (In Russ.).
17. Mitchell HH, Block RJ. Some relationships between the amino acid contents of proteins and their nutritive values for the rat. The Journal of biological chemistry. 1946;163:599–620.
18. Mitchell HH. Comparative nutrition of man and domestic animals. New York: Academic Press; 1964. 596–604 p.
19. Lipatov NN, Lisitsyn AB, Yudina SB. Sovershenstvovanie metodiki proektirovaniya biologicheskoy tsennosti pishchevykh produktov [Improving the methodology for designing the biological value of foods]. Meat Industry. 1996;(1):14–15. (In Russ.).
20. Lipatov NN, Lisitsyn AB, Yudina SB. Sovershenstvovanie metodiki proektirovaniya biologicheskoy tsennosti pishchevykh produktov [Improving the methodology for designing the biological value of foods]. Storage and Processing of Farm Products. 1996;(2):24–25. (In Russ.).
21. Lipatov NN, Lisitsyn AB, Yudina SB. Perevarimostʹ in vitro belkov nekotorykh vidov pishchevogo syrʹya [Digestibility of in vitro proteins in certain types of food raw materials]. Storage and Processing of Farm Products. 1996;(2):32–34. (In Russ.).
22. Ivashkin YuA., Yudina SB, Nikitina MA, Azarova NG. Informatsionnye tekhnologii proektirovaniya pishchevykh produktov [Information technologies for food design]. Meat Industry. 2000;(5):40–41. (In Russ.).
23. Titov EI, Rogov IA, Ivashkin YuA, Nikitina MA, Glazkova IV, Mitaseva LF. Ehkspertnaya sistema optimizatsii sostava produktov i ratsionov pitaniya [The expert system for optimizing the composition of foods and diets]. Moscow: MGUPB; 2009. 124 p. (In Russ.).
24. Krasnov AE, Krasulya ON, Bolʹshakov OV, Shlenskaya TV. Informatsionnye tekhnologii pishchevykh proizvodstv v usloviyakh neopredelennosti (sistemnyy analiz, upravlenie i prognozirovanie s ehlementami kompʹyuternogo modelirovaniya) [Information technologies for food production in uncertain conditions (system analysis, management and forecasting with elements of computer modelling)]. Moscow: VNIIMP; 2001. 496 p. (In Russ.).
25. Muratova EI, Tolstykh SG, Dvoretskiy SI, Zyuzina OV, Leonov DV. Avtomatizirovannoe proektirovanie slozhnykh mnogokomponentnykh produktov pitaniya [Automated design of complex multicomponent foods]. Tambov: Tambov State Technical University; 2011. 78 p. (In Russ.).
26. Smolikhina PM, Muratova EI, Dvoretsky SI. The study of structure formation processes in the confectionery mass. Advanced Materials and Technologies. 2016;(2):43–47. DOI: https://doi.org/10.17277/amt.2016.02.pp.043-047.
27. Musina ON, Lisin PA. System modeling of multicomponent foods. Food Processing: Techniques and Technology. 2012;27(4):32–37. (In Russ.).
28. Musina ON, Lisin PA. An approach to the choice of alternatives of the optimized formulations. Foods and Raw Materials. 2015;3(2):65–73. DOI: https://doi.org/10.12737/13120.
29. Musina O, Putnik P, Koubaa M, Barba FJ, Greiner R, Granato D, et al. Application of modern computer algebra systems in food formulations and development: A case study. Trends in Food Science and Technology. 2017;64:48–59. DOI: https://doi.org/10.1016/j.tifs.2017.03.011.
30. Borisenko AA. Algorithm of poly- components mixtures modeling with using a recursive cycle and referring to the relative database. Information Technologies. 2006;(7):69–71. (In Russ.).
31. Borisenko AA. Modern trends in the implementation of the convergence approach at development of meat products for a healthy diet. Newsletter of North-Caucasus Federal University. 2017;59(2):7–12. (In Russ.).
32. Prosekov AYu. Nauchnye osnovy proizvodstva produktov pitaniya [Scientific foundations of food production]. Kemerovo: KemIFST; 2005. 234 p. (In Russ.).
33. Prosekov AYu. Fundamentalʹnye osnovy tekhnologii produktov pitaniya [Fundamentals of food technology]. Kemerovo: Kemerovo State University; 2019. 498 p. (In Russ.).
34. Prosekov A, Petrov A, Lisitsyn A, Ulrich E, Dyshlyuk L, Dolganuk V. A selection of conditions for the biodegradation of poultry wastes industry. Research Journal of Pharmaceutical, Biological and Chemical Sciences. 2016;7(4):2762–2767.
35. Sanina TV, Serbulov YuS. Differentsirovannyy podkhod v kompleksnoy otsenke kachestva khlebobulochnykh izdeliy [A differentiated approach to a comprehensive quality assessment of bakery products]. Storage and Processing of Farm Products. 2004;(5):47–50. (In Russ.).
36. Zaporozhsky AA, Zaporozhskaya SP, Kovtun TV, Revenko MG. Researches perspectives in the sphere of herodietic products creation. News institutes of higher education. Food technology. 2012;326–327(2–3):5–9. (In Russ.).
37. Redko MG, Zaporozhskiy AA. Prospects of use of pigeons meat in production of gerodietetic products. News institutes of higher education. Food technology. 2016;349(1):21–24. (In Russ.).
38. Reznichenko IYu, Aleshina YuA, Galieva AI, Egorova EYu. Methodology of projection of confectionery products of functional purpose. Food Industry. 2012;(9):28–30. (In Russ.).
39. Reznichenko IYu, Chistyakov AM, Renzyaeva TV, Renzyaev AO. Development of recipes flour confectionery products of functional purpose. Bread products. 2019;(6):40–43. (In Russ.). DOI: https://doi.org/10.32462/0235-2508-2019-28-6-40-43.
40. Kiselev VM, Pershina EG. Evolution of methodology of functional food projection. Food Industry. 2009;(11):57–59. (In Russ.).
41. Musatov DV. Slozhnostʹ vychisleniy [The complexity of calculations]. Moscow: Moscow Institute of Physics and Technology; 2017. 224 p. (In Russ.).
42. Krasulya ON, Nikolaeva SV, Tokarev AV, Krasnov AE, Panin IG. Modelirovanie retseptur pishchevykh produktov i tekhnologiy ikh proizvodstva: teoriya i praktika [Modelling food formulations and their production technologies: theory and practice]. St. Petersburg: GIORD; 2015. 320 p. (In Russ.).
43. Krasulya ON, Tokarev AV, Grikshas SA, Shuvarikov AS, Pastukh ON. Intellektualʹnye ehkspertnye sistemy v praktike resheniya prikladnykh zadach pishchevogo proizvodstva [Intelligent expert systems in the practice of solving applied problems of food production]. Irkutsk: Megaprint; 2018. 152 p. (In Russ.).
44. Koneva MS, Usatikov SV, Bugaets NA, Tamova MY. Neural network and regression analysis of the dependence of the ranking score of organoleptic characteristics on the food system composition. Asian Journal of Pharmaceutics. 2017;11(2):S308–S319.
45. Berezina NA, Artemov AV, Nikitin IA, Budnik AA. The method of computer-aided design of a bread composition with regard to biomedical requirements. International Journal of Advanced Computer Science and Applications. 2019;10(5):137–143. DOI: https://doi.org/10.14569/IJACSA.2019.0100517.
46. Nikitina MA, Chernukha IM. Multi–criteria optimization of a product recipe composition. Theory and Practice of Meat Processing. 2018;3(3):89–99. (In Russ.). DOI: https://doi.org/10.21323/2414-438X-2018-3-3-89-98.