Аннотация

Microbial death kinetics modelling is an integral stage of developing the food thermal sterilisation regimes. At present, a large number of models have been developed. Their properties are usually being accepted as adequate even beyond boundaries of experimental microbiological data zone. The wide range of primary models existence implies the lack of universality of each ones. This paper presents a comparative assessment of linear and nonlinear models of microbial death kinetics during the heat treatment of the Alicyclobacillus acidoterrestris spore form. The research allowed finding that single-phase primary models (as adjustable functions) are statistically acceptable for approximation of the experimental data: linear – the Bigelow’ the Bigelow as modified by Arrhenius and the Whiting-Buchanan models; and nonlinear – the Weibull, the Fermi, the Kamau, the Membre and the Augustin models. The analysis of them established a high degree of variability for extrapolative characteristics and, as a result, a marked empirical character of adjustable functions, i.e. unsatisfactory convergence of results for different models. This is presumably conditioned by the particularity and, in some cases, phenomenology of the functions themselves. Consequently, there is no reason to believe that the heat treatment regimes, developed on the basis of any of these empirical models, are the most effective. This analysis is the first link in arguing the necessity to initiate the research aimed at developing a new methodology for determining the regimes of food thermal sterilisation based on analysis of the fundamental factors such as ones defined spore germination activation and their resistance to external impact.

Ключевые слова

Microorganisms, death kinetics, survival kinetics, sterilising effect, Alicyclobacillus acidoterrestris, model

ВВЕДЕНИЕ

Microbiological safety is one of the key tasks in developing food production technology [1–4]. Most existing solutions are based on microbial inactivation via chemical or physical methods, as well as competitive substitution of pathogenic and opportunistic pathogenic microflora with probiotic bacteria. At the same time, thermal sterilisation remains the most common way to achieve the required level of microbiological safety.

The first stage in developing the thermal sterilisation mode is traditionally the analysis of the microbial death kinetics in the medium of the product for which this mode is developed [5]. Microbiological studies are carried out under isothermal conditions and repeated at different temperatures. Then the experimental data are approximated with a particular model [6–8]. Naturally, the adequacy of the selected model to the experimental data confirms the adequacy of ideas about the microbial death kinetics in general and, in particular, regarding extrapolation at concentrations of microorganisms down to 1 CDU/g. Obtaining correct quantitative experimental microbiological data for these concentrations is associated with geometrically increasing resource intensity and experimental error.

According to Whiting and Bushanan, all mathematical models describing the microbial response to the external negative effects can be divided into three large groups – primary, secondary and tertiary models. Thus, primary models approximate experimental data of the microbial death kinetics under isothermal conditions as a function of processing duration. Secondary models connect primary models, approximating them as a function of additional factors, which include primarily the temperature of processing, when developing thermal sterilisation regimes. Tertiary models include the software implementation of secondary models [9]. However, we believe, it would be more logical if the adaptation of secondary models to non-isothermal sterilisation regimes within specified boundary conditions was referred to tertiary models.

The primary models of thermal inactivation of microorganisms broke into development at the turn of the XX^th century. Then, basing on the analogy with the first order chemical reaction, Chick, and later Bigelow presented a model reflecting the kinetics of the microbial death resulted from external adverse factors (Bigelow model) as a linear kinetic model of the first order [10, 11]. Bigelow showed later that in general the kinetics sought for can be adequately represented in semilogarithmic coordinates [12]. Due to the simplicity of form and further manipulations, this model has become classic:

where N is a trough concentration of microorganisms, CFU/g;
N₀ is an initial concentration of microorganisms, CFU/g;
k is the rate of microbial death kinetics (often defined as a constant), lg (CFU/g)·min^–1 (time may be expressed in s, h, etc.);
τ is a duration of processing, min (time may be expressed in s, hour, etc.).

This model is based on the assumptions that all cells of microorganisms have the same resistance to the thermal impact in the processed product, and their death kinetics complies with statistical regularities [9, 13]. As a result, the death of each individual cell is considered from the point of view of accidental inactivation of the ‘critical molecule’.

To avoid pure empiricalness, some researchers attempted to adjust the Bigelow model. They expressed the dependence of the microbial death rate on the temperature of the process similarly to the dependence of chemical kinetics on the activation energy according to the Arrhenius equation [5]:

where E₀ is activation energy, J/mol;
R is the universal gas constant (8.3144598 J/mol·K);
T_abs is the absolute temperature of the triple point of water (273.16 K);
T is the process temperature, °C.

However, Peleg et al. question the adequacy of this approach in their work [14]. They argue this with the cardinal difference of the microbial death kinetics from the conventional chemical kinetics. The difference manifests itself in the absence of microflora inactivation under normal conditions and, therefore, in absence of continuity of functional dependence of microbial concentration on temperature over the entire range of its determination.

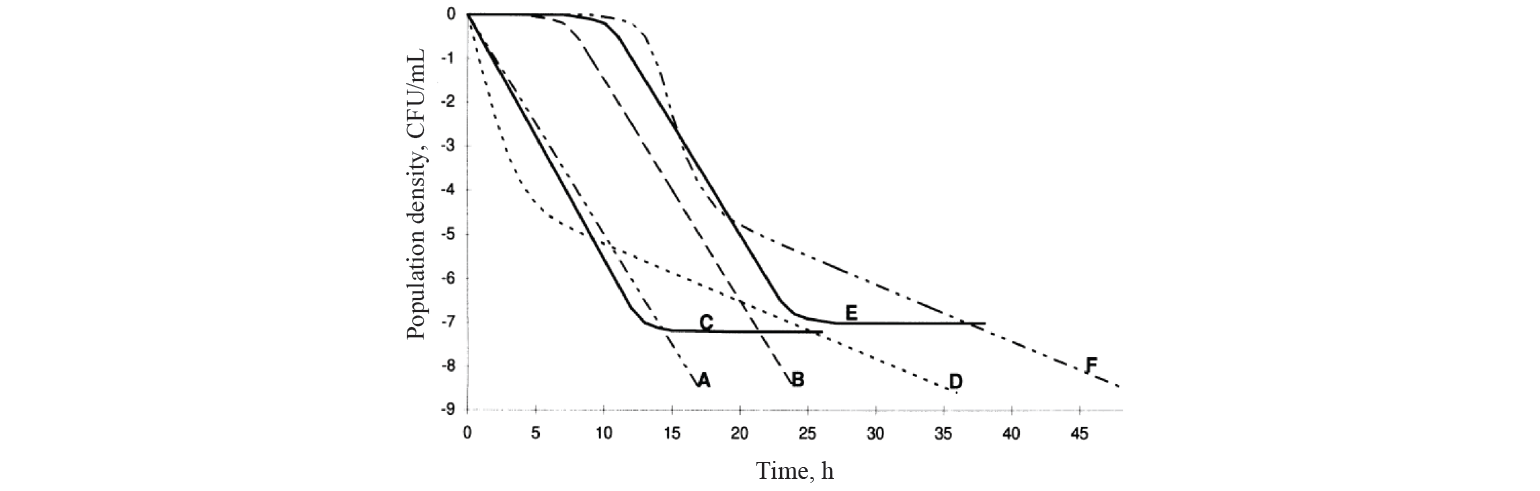
Nowadays, there are at least four main types of kinetics of microbial death as a result of heat treatment, including linear (Fig. 1) [15].

Kinetics with a lag phase is one of the frequent deviations of microbial death kinetics [16]. This type of dependence approximates satisfactorily the Whiting-Buchanan model proposed by Whiting and Buchanan [17, 18]:

where τ_lag is a lag phase duration.

Van Boekel carried out a large-scale study and analysed more than 120 curves of microbial death kinetics. He concluded that linear models described no more than 5 percent of cases. It implies that this kinetics is an exception rather than the rule [19]. Van Boekel suggested that non-linear models should be used for the most adequate description of kinetics. It should be understood that nonlinearity of models is determined primarily by their parameters, since the graphical representation resulting from approximation can have both nonlinear and linear views [16]. The simplest nonlinear model, the Weibull model, is based on the idea of statistical distribution of probability for the death of cells and/or microbial spores under the adverse external conditions as a result of their individual variability [20]:

where δ is a coefficient.

It is notable that at P > 1 the model represents a convex curve, while at P < 1 the curve is concave. When P = 1, the model becomes identical to the Bigelow model. The coefficient δ becomes equivalent to the value of D in the interpretation of the same model. It probably gave Mafart a reason to adopt the coefficient δ as the duration of the process required to reduce the microbial concentration by one order [20].

Bhaduri et al. [21] were the first who showed that the empirical modified Gompertz equation, the Gompertz model, can effectively describe the thermal death kinetics of Listeria monocytogenes:

where C, b and M are coefficients.

A little earlier, Casolari [22] proposed a model that satisfactorily approximates the microbiological data of kinetics with ‘tails’, i.e. the first Casolari model:

where b_T is a coefficient.

He linked the microbial death to the critical activity of water molecules when their energy exceeds a threshold value E0, thus combining the probability theory and Maxwell energy distribution:

where N_a is Avogadro’s constant (6.022140857×10²³, mol^–1);
M_H20 is molar mass of water (18.01528 g/mol).

In the same work and later in [6, 23] was presented the modification of this model, i.e. the second Casolari model. It included a quadratic dependence on the processing duration:

In their turn, Daugthry et al. [24] proposed an exponentially decreasing model, i.e the Daugthry model. They justified its advantage over linear models due to the approximation accuracy of the experimental data on the death kinetics of Escherichia coli and Staphylococcus aureus

where k is the initial rate of inactivation;
λ_d is the descending factor.

Data in [25, 26] demonstrate the expediency of a logistic function, i.e. the Fermi model, for describing the kinetics of microbial death limited by a number of stressful factors:

where τ_lag is a lag phase duration.

Cole et al. [27] proposed a four-factor logistic model, i.e. the Cole model:

where ω is the value of the lower asymptote of microbial death kinetics, lg (CFU/g);
σ is the maximum rate of kinetics.

The model satisfactorily described the thermal inactivation of Salmonella typhimurium, Cl. botulinum, Salmonella enteritidis and E. coli.

Membre et al. proposed a modified logistic function, the Membre model, to describe the thermal inactivation of Salmonella typhimurium. They assumed that the model could extrapolate on other microorganisms and products [28]:

Another kinetic model, the Kamau model, is proposed by Kamau et al. [29] in relation to Listeria monocytogenes and Staphylococcus aureus:

where k_d is a coefficient.

The complex logistic model, the Baranyi model, was developed as an alternative to the Gompertz model described by formula (5). It takes into account the advantages of the Gompertz model and levels its disadvantages. Xiong et al. [30] modified the Baranyi model, which took the form:

where q_b is an indicator of the ‘tail’ of kinetics, reflecting its manifestation or absence;
μ_m is a maximum relative level of thermal inactivation;
r is a lag parameter, numerically equal to half μ_m;
B_T is a coefficient.

A distinctive feature of the Baranyi model is the possibility to derive the kinetic model of the first order on its basis.

Geeraerd et al. [23] proposed the Geeraerd model as a complex approach to describing the complex kinetics of thermal microbial inactivation. The model takes into account the presence or absence of the ‘tail’ of the function, and also a lag phase in microorganisms responding to the thermal effect:

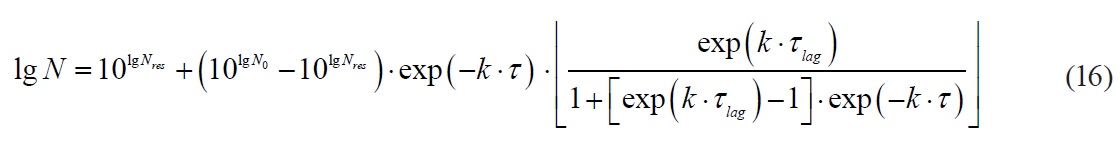
The analysis of these models shows that in many cases logistic functions are mathematical abstractions that describe experimental microbiological data more or less satisfactorily. The Augustin model proposed in [31] and originally intended to describe the kinetics of thermal inactivation of Listeria monocytogenes is no exception

where m and s are coefficients.

However, due to the commonality of this model with other logistic functions, this model may be ostensibly applicable to the description of thermal inactivation kinetics of other microorganisms.

The Fernandez model stands apart. It was proposed in [32] and based on the statistical approach to estimating the density of distribution:

A new empirical nonlinear model was developed, i.e. the Chiruta model [33]:

where a, b and c are coefficients.

The model is a modified polynomial function with all properties characteristic of approximation functions of this class. The properties are satisfactory interpolation and sensitivity to approximated data. Extrapolation of this model is possible, but it must be carried out with caution and mandatory experimental validation.

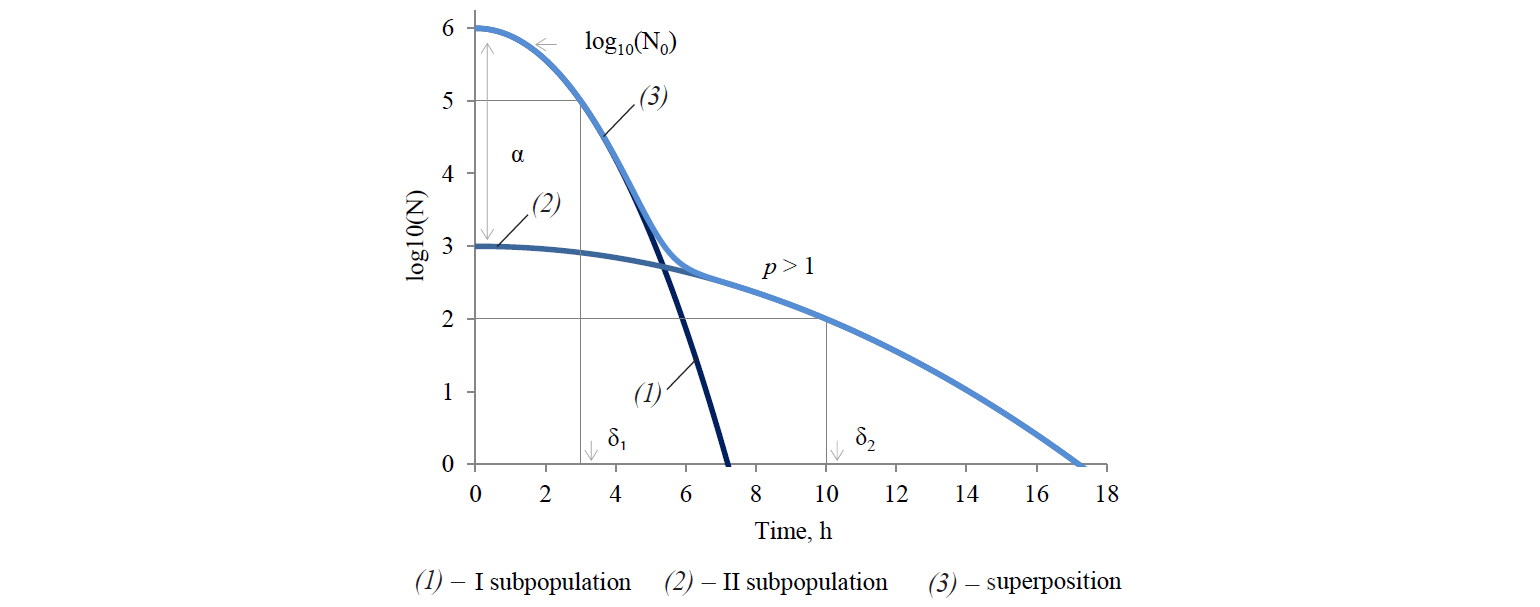
Analysing the existing array of the experimental microbiological data, Cerf [34] was one of the first to who suggested that the deviation of kinetics from linear (in semilogarithmic coordinates) is most likely a consequence of simultaneous presence of at least two microbial subpopulations with different resistance to external negative effects in a genetically homogeneous population. The deviation may also be caused by artefacts (generated by a set of perturbation factors that are not taken into account, or are not levelled in the formulation and execution of studies). Figure 2 presents a graphical interpretation of this approach.

In relation to thermal inactivation kinetics, the result of this conclusion is the use of two-phase models, taking into account the contribution of each subpopulation to the integral response. Models of this kind were developed by Geeraerd et al [23], Kamau et al [29], Xiong et al [30], Cerf [34], Whiting and Buchanan [35], and Coroller et al [36].

The Cerf model is described by the formula:

where f is a share of the first subpopulation in the test culture;
1 and 2 are indices of coefficients belonging to the subpopulation.

The Kamau model is described by the formula:

The Whiting-Buchanan model:

The Coroller model:

The Xiong model:

where

The Geeraerd model:

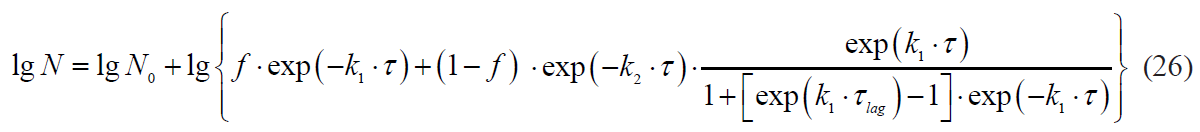
Theoretically, there may be a significant difference in the concentration of subpopulations (10 or more times). As a result, the calculation of the share of the first subpopulation f may be complicated due to its small correction from unity. To solve this problem, Geeraerd proposed to substitute the indicator f with its more variable form:

Then:

A wide variety of primary models implies the lack of universality of each of them. It turns the application of such models into their adjusting to specific experimental data of microbial thermal inactivation kinetics. At the same time, it is still unclear whether the results of extrapolating these models outside the scope of determining the experimental values of input and output factors are adequate. The adequacy can be partly justified with the arguments by the authors of the models. However, as the authors of the models suggested, the arguments are also very empirical.

Accordingly, the issue of adequate applicability or non-applicability of empirical approaches to determining thermal sterilisation regimes requires comparative assessment of models and modes predicted with the help of the approaches. The convergence of their results as well as compliance with the existing trends of the development of food technologies and requirements for quality and safety of food products should be taken into consideration.

Thus, the aim of this work was to analyse the convergence of existing approaches to modelling the microbial death kinetics during heat treatment. To achieve this goal, we solved the following tasks:

– an analytical review of existing approaches to modelling the microbial death kinetics during the heat treatment;
– a comparative evaluation of (a) primary kinetic models of microbial spore death; (b) secondary kinetic models of microbial spore death; and (c) models describing rate dynamics of microbial death kinetics.

ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ

The research focused on the following objects: the spore form of the guaiacol-positive strain of Alicyclobacillus acidoterrestris RNCIM V-1008 from the centre for culture collection of microorganisms, the Laboratory of Quality and Food Safety of the Russian Research Institute of Canning Technology.

The spore suspension of A. acidoterrestris was prepared according to [37]. For this purpose, the culture from the collection was activated by means of double or triple relocation to the liquid nutrient enrichment medium, i.e. the YSG medium (HiMedia Laboratories Pvt. Ltd., India). Subsequently, the actively growing daily culture was planted into Petri dishes with pre-prepared BAT-agar (HiMedia Laboratories Pvt. Ltd., India).

For this purpose, 0.1–0.2 cm³ of the cell culture fluid was evenly distributed on the surface of the medium with a spatula. The platings were thermostated at 40°C for 96 h. To detect the spores, the native sample was studied with phase contrast microscopy, using the Zeiss Axioscope microscope, equipped with Canon PC 1200 camera and original AxioVision Rel.4.8 software. The culture contained light refractive shiny spores. Their amount was not less than 70% compared to the total number of cells. The spores produced on a solid nutrient medium were washed off with a phosphate buffer (0.1M aqueous solution of phosphate buffer, pH 6.98), according to [38], approximately 10–15 cm³ solution per 75 cm² surface. The spores were separated from the medium by centrifuging the culture fluid at 275 g for 30 min. Washing and centrifuging were repeated several times.

The washed sediment was suspended in the medium of concentrated apple juice. The resulting suspension had a spore concentration of not less than 107 CFU/g. To inactivate the remaining vegetative cells, the suspension was heated at 80°C for 10 min. The concentration of spores in the suspension was determined by plating appropriate dilutions on BAT-agar within Petri dishes. The obtained suspension was used to determine the parameters of thermal stability in the concentrated apple juice (ACJ).

The capillary method was used to determine the parameters of thermal stability of the spores in the studied juice. For this purpose, the medium was contaminated by applying the spore suspension in sterile conditions. The capillaries were thin-walled glass tubes, 75 mm long, outer diameter of 3 mm. The spore suspension was injected into capillaries by 0.1 cm³. Each capillary contained spores at a concentration of 5.31 lg(CFU/g). The filled capillaries were warmed up in the circulating thermostat series LOIP LT-311 (Russia) in the glycerine medium at 100°C and over and the aqueous medium at temperatures below 100°C.

The contaminated samples were thermostated in capillaries at 90 and 95°C for 420 s, 100°C for 300 s, and 105°C for 150 s. The trough concentration of the surviving spores was established after 0, 120, 240, 360 and 420 s for 90 and 95°C; after 0, 60, 120, 180, 240, and 300 s for 100°C, and after 0, 30, 60, 90, 120, 150 s for 105°С. The trough concentration of the surviving spores was determined according to [37] by direct inoculation method. The samples of 1 cm³ were analysed using YSG-agars as dense nutrient media. The initial processing of the inoculation results was carried out according to [39]. All microbiological studies were carried out in four-fold repetition, rejecting statistically unreliable data.

To determine the dynamics of heating the ACJ in the least heated zone, the sterile medium was placed in a glass jar of 100 cm³ with a twist-off lid and a thermocouple element fixed by a vertical axis of the jar, 15 mm off the inside surface of the bottom. Hermetically sealed jars with ACJ were thermostated at 90, 95, 100 and 105°C.

The temperature was measured in the least heated point at 30-second intervals for 42 min. After that, the jars were cooled in a water tank at 15°C for 10 min. The automatic multichannel thermometer CTF9008 (Ellab A/S) connected to the thermocouples was used for temperature control during the heat treatment. To reduce statistical error, each experiment was carried out in a three-fold repetition, rejecting statistically unreliable data.

Mathematical processing and modelling was carried out using a spreadsheet processor Microsoft Excel 2010 (Microsoft Corporation) with installed add-ons ‘Data Analysis’, ‘Solution Search’ and ‘Parameter Selection’, as well as specialised software — TableCurve 2D v.5.01 (SYSTAT Software Inc.) and Wolfram Mathematica 10.4 (Wolfram Research Inc.).

Approximation of the experimental data was carried out under the following parameters of TableCurve 2D Fitting Controls option of TableCurve 2D v.5.01: linear approximation was by Singular Value Decomposition; the level of robustness (stability) of nonlinear approximation was high (Pearson VII Lim); minimisation by natural logarithm of the square root of the sum ‘1 + squared remainder’.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Comparative evaluation of primary kinetic models of the microbial spore death. The literary data review showed that at present a basic provision underlying any approach to determining the thermal sterilisation regimes for canned products is experimental determination of the microbial death kinetics in the analysed product with the subsequent approximation and extrapolation of the obtained model. Therefore, the initial criterion for assessing the adequacy of the particular primary model application to describe experimentally fixed kinetics is the convergence of approximating (averaging) and interpolating properties (corresponding to the numerical values in the nodes, i.e. experimental points).

In the first approximation, this criterion is numerically equivalent to the determination coefficient, i.e. the square of the correlation coefficient. However, not all models can be calculated directly. Thus, in this study, linearising transformations were carried out previously for a number of models, i.e. the Kamau model, the Membre model and the Augustin model:

– the Kamau model

– the Membre model

– the Augustin model

The lower threshold of the determination coefficient of 0.9 was adopted as a boundary condition determining the applicability of the primary model for approximation of the experimental data.

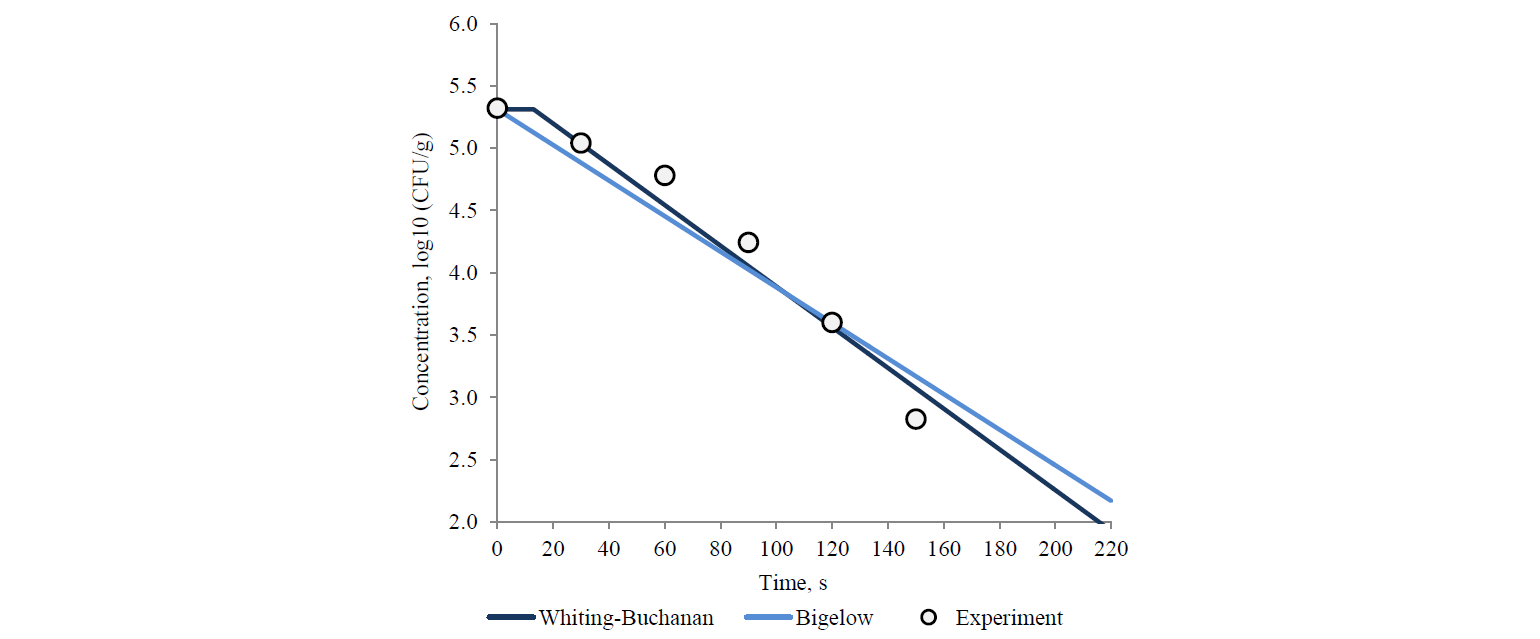
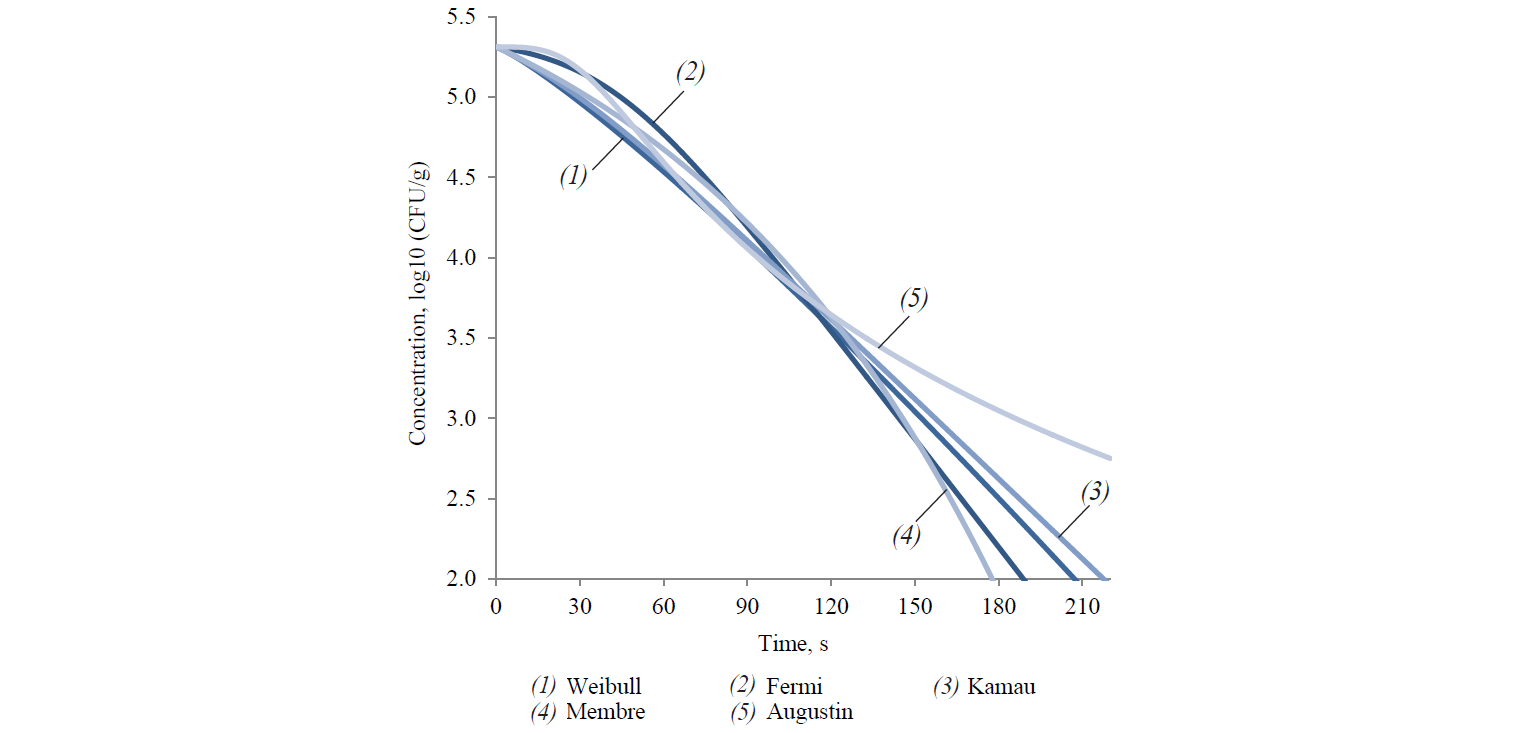
Thus, out of the described set of primary models, only seven models complied with the experimental data of survival kinetics of A. acidoterrestris. There were two linear models (the Bigelow model and the Whiting-Buchanan model) and five nonlinear models (the Weibull model, the Fermi model, the Kamau model, the Membre model and the Augustin model). In addition, in order to expand the potential of the primary models used for the Bigelow model, the activation energy of the microbial spore death was calculated in each of the temperature options according to Arrhenius. That indirectly increased the number of analysed models. At the same time, both the Bigellow model and its modification by Arrhenius in its primary form were actually identical.

The analysis of the study results showed a somewhat larger aggregate (for all temperature variants) adequacy of nonlinear models at experimental data approximation (Table 1). Thus, the determination coefficient did not fall below 0.965 for all temperature variations in nonlinear models. On the other hand, this coefficient decreased up to 0.936 and 0.956 for the Bigelow model and the Whiting-Buchanan model, respectively, in linear models. The non-linear Membre model was the only exception, comparable in aggregate adequacy to the Whiting-Buchanan model.

It is noteworthy that the activation energy of the microbial death, corresponding to the Bigellow model as modified by Arrhenius, was not constant. When the processing temperature was increasing, this value was monotonously decreasing, which presumably confirms the fact that many factors impact microbial resistance to external adverse conditions. When the temperature increases within the range of values corresponding to proteins denaturation, the number of such factors inevitably decreases. As a result, less energy is required to reach the target effect of the microbial death.

Table 1 presents characteristic indicators and determination coefficients corresponding to linear and non-linear models.

Table 1 demonstrates the heterogeneity of the approximation efficiency for any of the selected models within the temperature values in the experiment variants. It should be noted for most nonlinear models (except the Augustin model) that the approximation adequacy decreases when the linearity of experimentally determined kinetics increases and vice versa. The latter was established by the determination coefficient increase for linear models. It proves a low universality of the primary (in fact – adjustable) models. The consequence is an increase in the deviation of model-predicted values of the surviving microbial spore concentrations when extrapolating from the experimental data, intuitively expected on the basis of visual estimation (Figs. 3 and 4).

Thus, at 105°C, extrapolating both linear and most non-linear models towards increasing the duration showed lower heat treatment efficiency than it was intuitively assumed from the visual estimation of experimental data. It is true even for the Augustin model, approximating experimental data as formally adequately as possible. Conclusions were formed on the basis of modelling microbial death kinetics under thermal influence and its subsequent extrapolation. They were expressed in the form of the ratio of temperature and duration of treatment to achieve a given sterilising effect. Though, as a result of the above said, the conclusions will be inevitably overrated against the true state of affairs.

Thus, finding the primary model satisfying all variants of experimentally established kinetics even in the field of determining variable independent factors is a non-trivial problem. This problem appears in conditions of empiricism and simplification, and in many cases phenomenology of both existing primary models and approaches to their development. This conclusion is compounded by the ambiguity of extrapolating properties of the models. However, the whole further algorithm of determining the sterilisation regimes was built on these properties.

Comparative evaluation of secondary kinetic models of the microbial spore death kinetics. The numerical values of coefficients for primary microbial death models are different when calculated as a result of approximation of experimental data at different temperatures of heat treatment. It suggests some dependence of these values on temperature. The format of primary models has a certain logic though simplified. Unlike them, the functional dependencies of these models coefficients on the processing temperature are exclusively adjustable functions. These functions approximate an array of numerical values most efficiently and extrapolate logically. They extend the value of the independent factor in any direction beyond the scope of determining experimental values.

Thus, the coefficients of linear primary models depend on temperature as follows:

– the Bigelow and Whiting-Buchanan models:

– the Bigelow model:

– the Whiting-Buchanan model:

– the Bigelow model as modified by Arrhenius:

This approach resulted in differences in functional description of secondary models: the Bigelow model and the Bigelow model as modified by Arrhenius. The coefficient k carried the function of the kinetic rate of the thermal microbial death and in the first case it depended on temperature linearly (in semilogarithmic coordinates). Conversely, in the second case, this dependence acquired nonlinearity due to the complex of activation energy and the processing temperature. The activation energy itself had a linear dependence on the processing temperature in semi-logarithmic coordinates:

The coefficients of nonlinear primary models depended on temperature as follows:

– the Weibull model:

– the Fermi model:

– the Kamau model and the Membre model:

– the Augustin model:

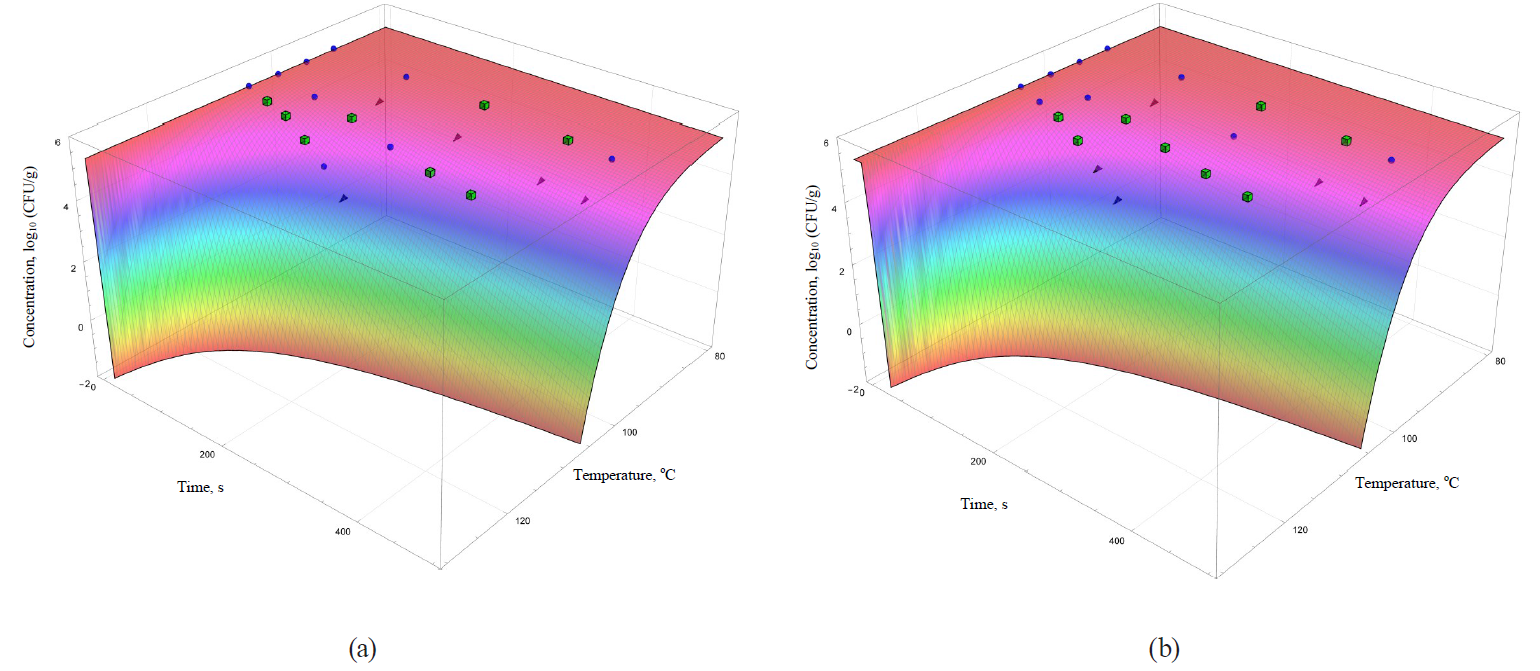
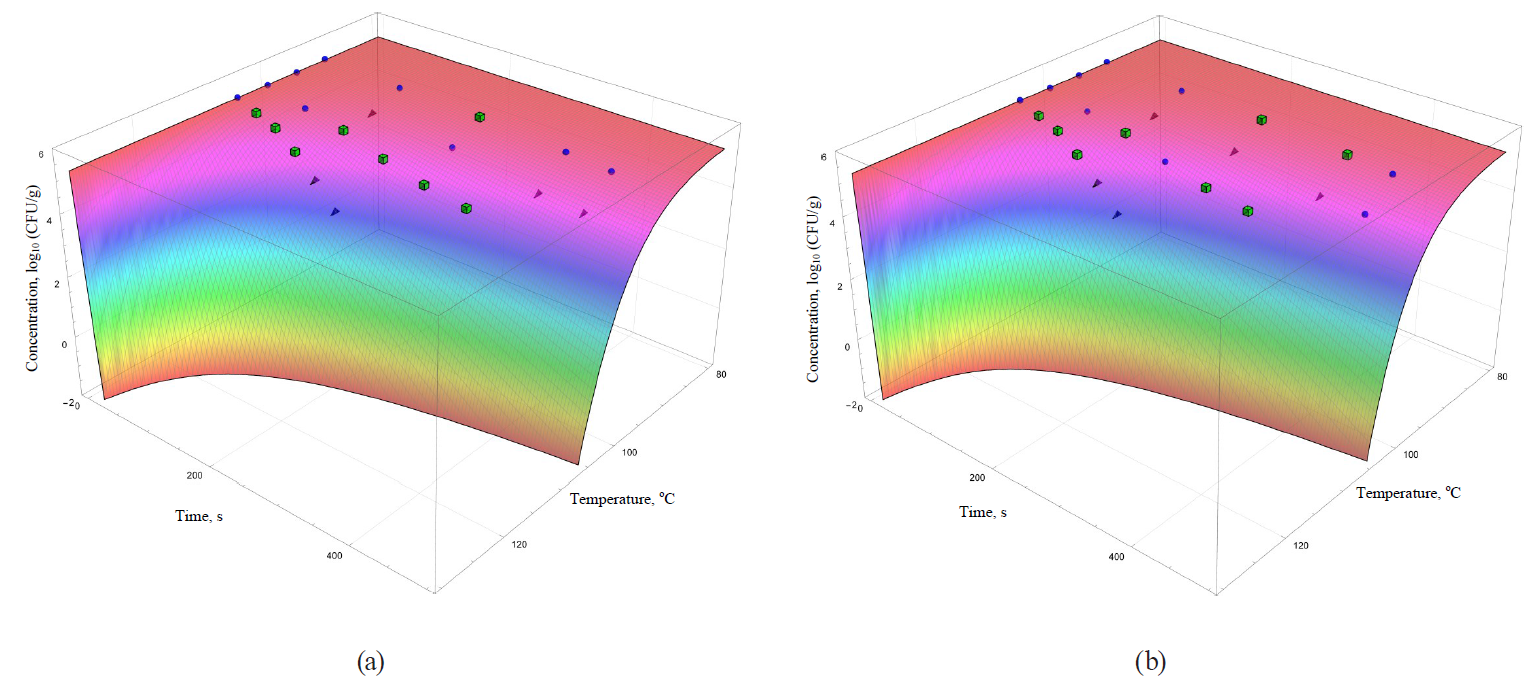
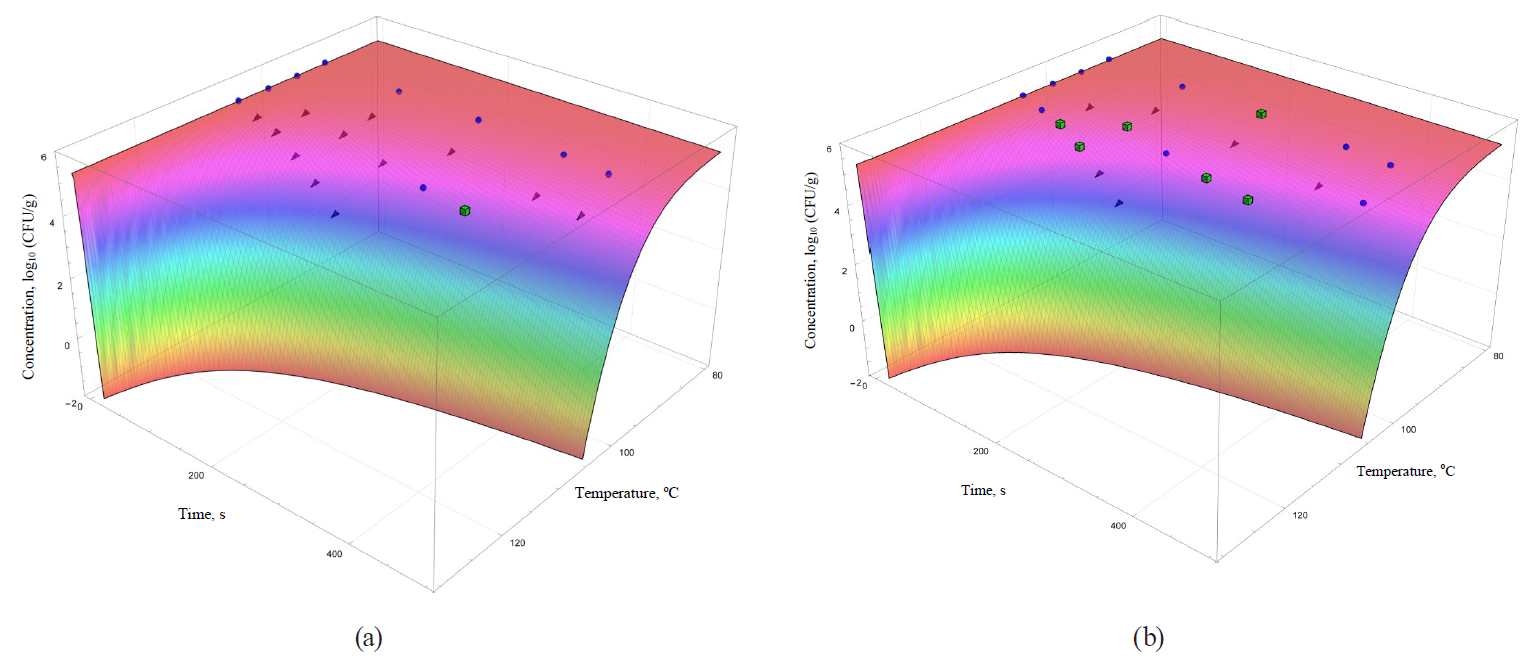
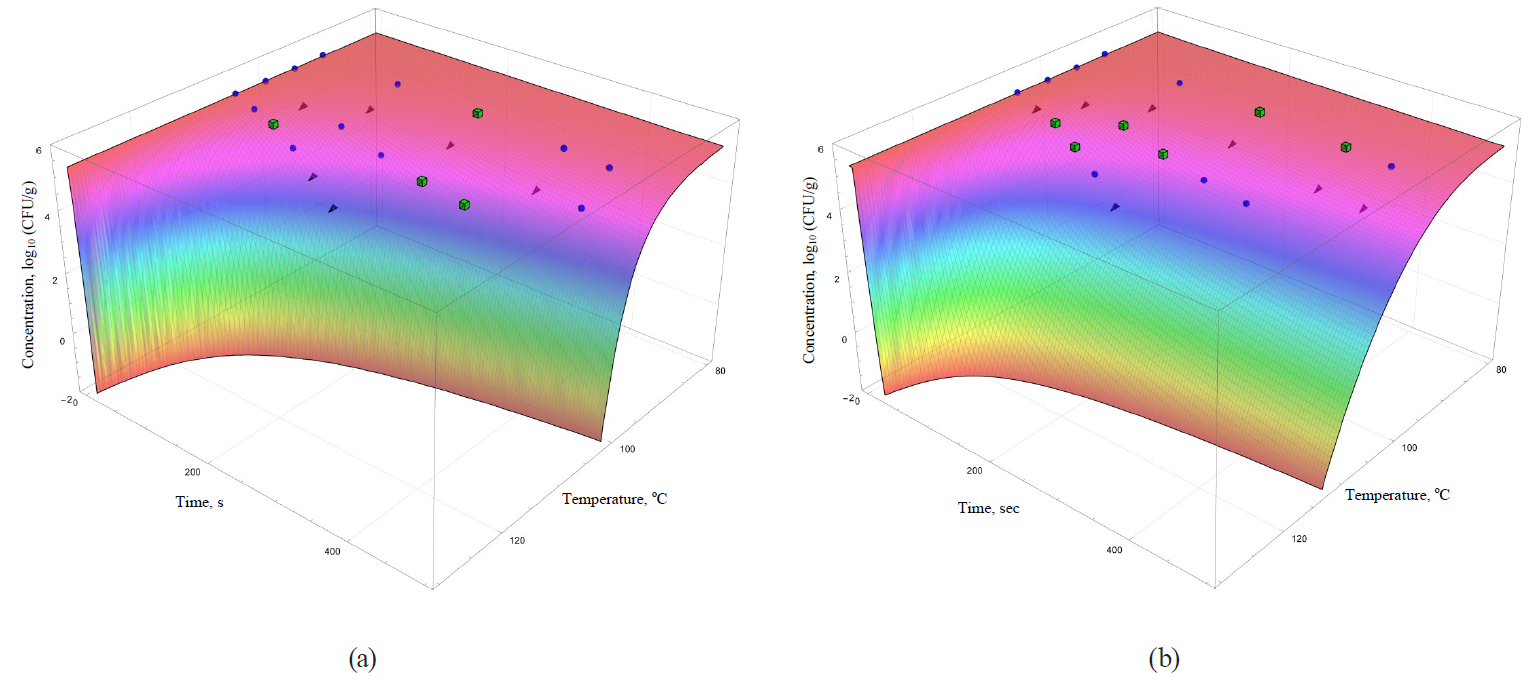
The coefficients are functionally expressed through formulae (32)–(42). In general, they allowed obtaining more informative – secondary – analogues for each of the analysed primary models (Figs. 5–8).

It is mandatory to bear in mind that primary models represent some degree of approximation of the functional idea of the microbial death dynamics as a result of thermal effect at the specified temperature.

In its turn, the functional dependence of coefficients on temperature allows determining their values in the process of inter- and/or extrapolation with a certain degree of approximation as well. Piling up with the error generated by the primary model, it determines the total degree of approximation to the experimental data in determining the temperature and processing time. This also sets some uncertainty in further extrapolation. The consequence of this conclusion presents itself in the degree to which secondary models comply with the experimental data on the basis of which these models were obtained.

The models were superimposed on the array of experimental microbiological data in Figs. 5–8. Colour variations indicated the consistency of experimental data, taking into account their errors, and the model. The green cubes show experimental data that exceeded the concentration of the surviving microbial spores calculated on the basis of the model. Black triangles show the data having values below the calculated ones. Blue spheres indicate values the same as the model within the error range of experimental data.

The analysis of the convergence of experimental data and models showed that there is a poor convergence with the kinetics at 95°C in the case of linear primary models. In addition, the secondary models – the Whiting-Buchanan model (Fig. 5b) and the Bigelow model as modified Arrhenius (Fig. 6a) – showed a greater progression in the microbial death kinetics at 100°C compared to the kinetics as determined by the experimental data. However, these same models showed unsatisfactory extrapolative properties at 105°C towards overrating the concentration of the surviving microorganisms.

There was even a greater heterogeneity in the case of secondary models based on nonlinear primary models. Thus, the secondary model based on the Fermi model (Fig. 7a) has the visually worst approximation properties and, as a consequence, extrapolative characteristics. This model overestimates the calculated concentration of the surviving microorganisms for the most part in comparison with the experimental values. The Weibull model (Fig. 6b) is characterised by almost the same disadvantages as those noted for the Whiting-Buchanan model and the Bigelow model modified by Arrhenius.

The same statement, but to a lesser extent, can be applied to the secondary models, i.e. the Kamau model (Fig. 7b) and the Membre model (Fig. 8a). Of all secondary models, the Augustin model was the most appropriate in terms of convergence with the experimental data. However, it was also characterised by overestimating the calculated values of surviving microbial concentration at the treatment temperature of 95°C, as well as overestimating the calculated values at extrapolation at the temperature of 105°C.

However, the graphical analysis of the secondary models showed that each of them was characterised by the continuous area in the ‘duration – temperature’ coordinates. It was true for this area that a trough concentration of surviving microbial spores reached the value, not exceeding a given threshold. This fitted well into the formal logic that ‘a higher temperature value corresponds to a shorter processing time’. In Figs. 5–8, the trough concentration of surviving microbial spores of 10^–2 CFU/g was randomly chosen as such threshold value. It corresponded to the sterilising effect of reducing microbial concentrations from the initial value by more than seven orders.

Comparative evaluation of rate dynamics models for microbial death kinetics. The graphical display of the secondary models was characterised by external homogeneity (if connection to the experimental data was removed). However, the key factor for the overall microbial death kinetics was the change rate indicator of concentration of the surviving microorganisms after the heat treatment. The process rate was defined as a value derived from the kinetics of the analysed index (in this case, the concentration of microorganisms).

Therefore, if there was a functional dependence reproducing the kinetics of the analysed index, the rate could be defined as the first time derivative. If the dynamics of microbial concentration increase was negative, which occurred during heat treatment, the rate value was also be negative. However, for greater convenience and clarity without levelling adequacy, we used the rate value with the opposite sign in further calculations and representations. Thus, the rate of microbial death kinetics corresponding to the secondary models could be expressed as the following:

– the Bigelow and Whiting-Buchanan model:

where υ is the rate of microbial death kinetics, lg (CFU/g) /s;

– the Bigelow model modified by Arrhenius:

– the Weibull model:

– the Kamau model:

– the Fermi model:

where a_b is the coefficient corresponding to the coefficient a in formula (38);
b_b is the coefficient corresponding to the coefficient b in formula (38);
a_τlag is the coefficient corresponding to the coefficient a in formula (39);
b_τlag is the coefficient corresponding to the coefficient b in formula (39);

– the Membre model:

– the Augustin model:

where a_m is the coefficient corresponding to the coefficient a in formula (41);
b_m is the coefficient corresponding to the coefficient b in formula (41);
a_s is the coefficient corresponding to the coefficient a in formula (42);
b_s is the coefficient corresponding to the coefficient b in formula (42).

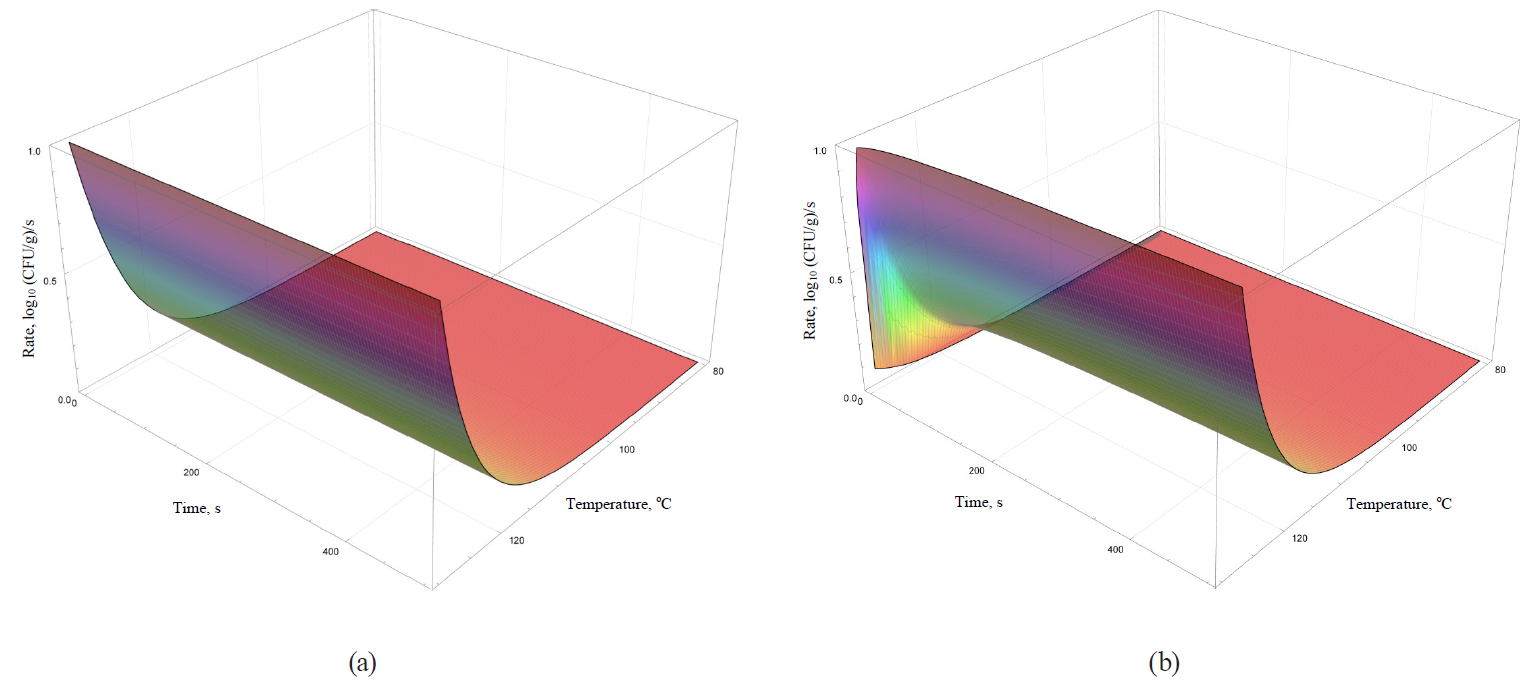
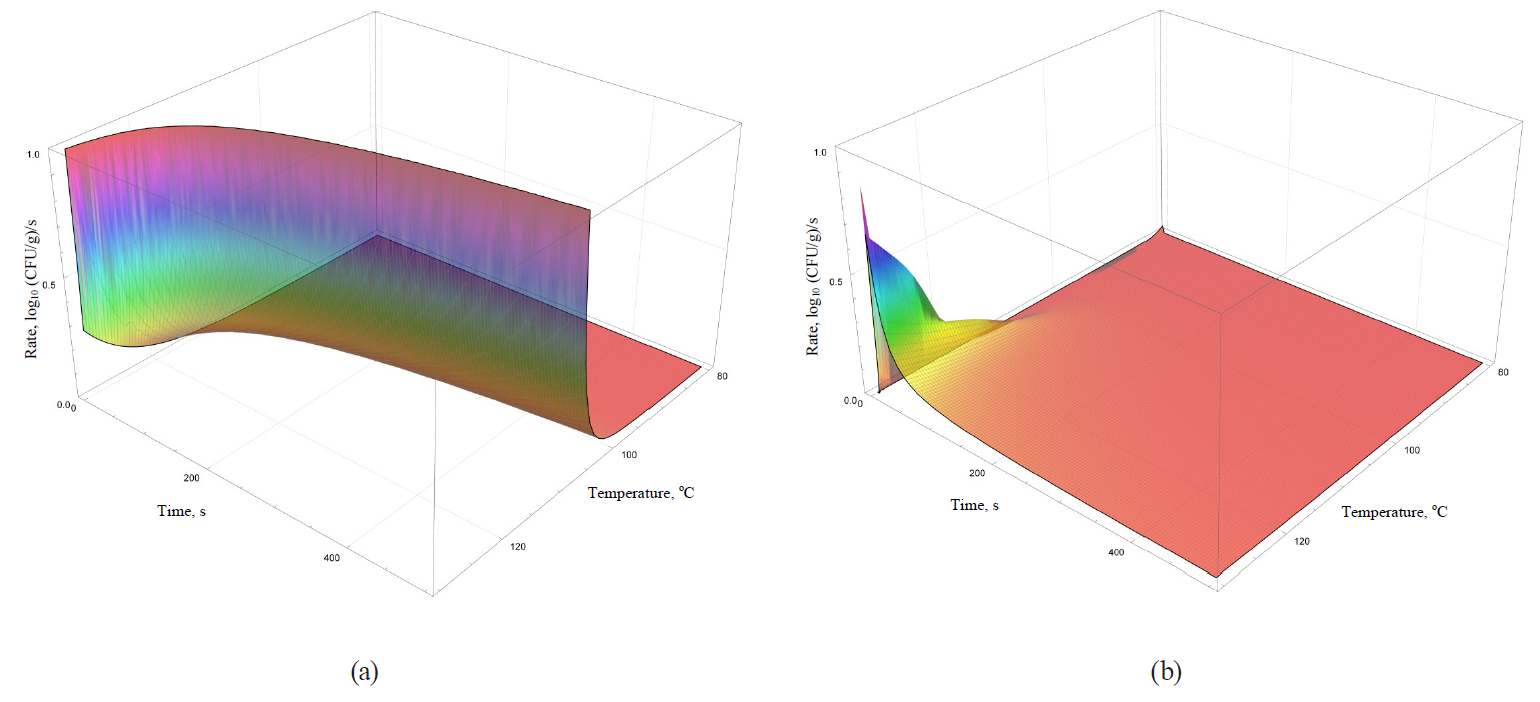
Models of the rate dynamics for microbial death kinetics during the heat treatment are featured in Figs. 9–12.

Analysis of formulae (43)–(49) and their graphical representation showed that all linear models (Figs. 9 and 10a) were invariant in terms of the heat treatment duration, while nonlinear models (Figs. 10b, 11, 12) included the time component.

The rate growth intensity of microbial death kinetics differed visually almost twice even in externally similar linear models, such as the Bigelow model and the Bigelow model modified by Arrhenius. It occurred within graphically represented area of temperature determination of the heat treatment (80–130°C).

Some nonlinear models (the Weibull model, the Fermi model and the Kamau model) demonstrated a pronounced effect of treatment duration on the rate of microbial death kinetics only at the initial stages of processing at temperatures over 100°C. For others (the Membre model), the rate was determined by the pronounced effect of both factors on the entire graphically represented area of determination. In the Augustin model, the rate dynamics decreased to zero by increasing both temperature and the processing duration.

Presumably, these differences did not have any profound fundamental effect due to the initial representation of the primary models in question. The models were used for further constructions as adjustable (empirical) functions that were not bound to fundamental aspects, i.e. molecular and possibly supermolecular mechanisms, which directly determine the spore resistance to thermal treatment.

The dependence of the rate dynamics for microbial death kinetics on the processing duration for nonlinear models results in the need to determine the formal starting moment of the heat treatment. This moment should serve the starting point for measuring the real duration in order to determine the actual values of the sterilising effect for each temperature value obtained during the experimental heating. Indeed, the initial (starting) concentration of microbial spores in the product in the real conditions of thermal sterilisation was significantly (by 5–8 orders) lower than their initial concentration in microbiological experiment of heating the contaminated product. Then, in general terms, the conditions for achieving the starting microbial spore concentration and the final concentration achieved at an arbitrary time point under the known functional dependences which approximated microbiological data satisfactorily, we got the following form:

where N_st is a starting microbial spores concentration in the product, CFU/g;
τ_st is a theoretical duration of the heat treatment to achieve the starting microbial concentration according to the selected model (starting treatment duration), s.

In this case, at an arbitrary time point, the sterilising effect n was defined as:

The obvious consequence of formula (51) was the conclusion that reaching n ≥ 0 required fulfilling the condition τ ≥ τ_st.

To simplify the calculations in this study, the starting microbial spore concentration was assumed equal to 1 CFU/g. Then lg N_st = 0. In this case n = − f ( τ ,T ). This conclusion could be used in the calculation of sterilising effects at each temperature value. For this, the calculated sterilisation duration for each given temperature value at the real moment of determination, adjusted to τ_st, must be substituted into the formula of the rate of microbial death kinetics.

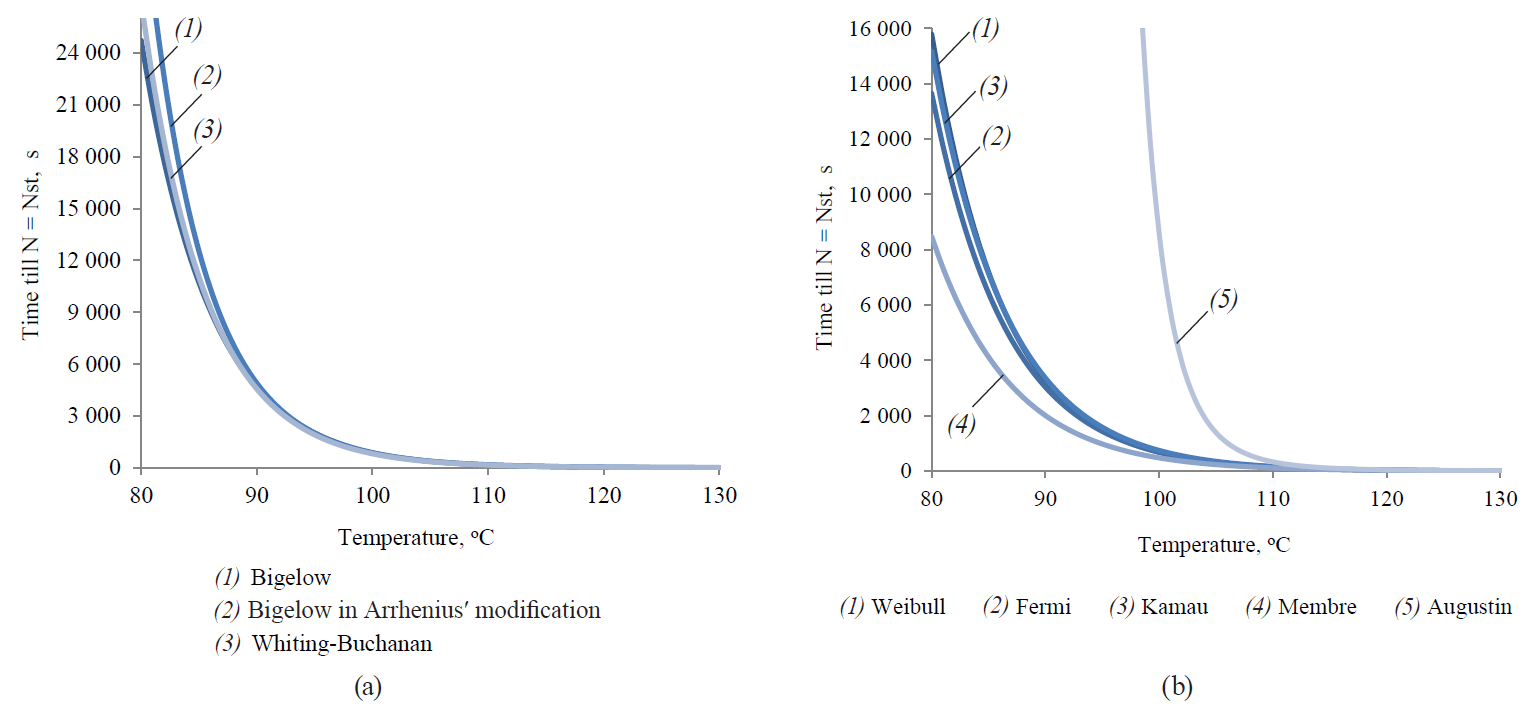
The analysis of secondary models showed that for a given N_st value τ_st was a function of the process temperature. However, due to the peculiarities of formulas describing secondary models, not each of them could have an explicit form of dependence. In this regard, the ratios {T, τ_st} in the area of temperature determination from 80 to 130°C were numerically determined for each model. Then they were approximated with the following functions:

– the Bigelow model, the Weibull model, the Kamau model and the Membre model:

– the Bigelow model modified by Arrhenius:

– the Whiting-Buchanan model and the Fermi model:

– the Augustin model:

Figure 13 shows graphical representations of functional dependences of τ_st on temperature, corresponding to both linear and non-linear models.

The visual analysis showed a relatively high degree of variability of this dependence for nonlinear models. It indicated the pronounced variability in the dynamics of extrapolative properties for the different models studied due to the expressed empirical character of the adjustable functions. In its turn, this variability was presumably conditioned by the particularity and, in some cases, the phenomenological nature of the functions themselves, while there was no adequate connection with the fundamental mechanism of microbial spore inactivation. In addition, this variability must inevitably lead to the significant variability of the final regimes of thermal sterilisation. The regimes could be determined by applying the analysed models to the same array of initial microbiological and thermophysical data.

ВЫВОДЫ

According to the results of the research and subsequent analysis, the single-phase primary models (adjustable functions) are statistically acceptable (at r² > 0.9) for approximation of experimental data on the kinetics of thermal death of Alicyclobacillus acidoterrestris spores. The models were linear, namely the Bigelow model, the Bigelow model modified by Arrhenius, and the Whiting-Buchanan model, and nonlinear, such as the Weibull model, the Weibull model modified by Malfart et al., the Fermi model, the Kamau model, the Membre model, and the Augustin model. At the same time, nonlinear models approximate experimental microbiological data on death kinetics of microbial spores during the heat treatment statistically more adequately.

The unsatisfactory convergence of extrapolation results and dynamics caused by the rate models and the temperature coefficient was shown for the first time. In other words, the expressed empirical use of adjustable functions was established analytically. This was presumably conditioned by the particularity and, in some cases, phenomenology of the functions themselves. Other causes were the lack of the criteria for the unambiguous choice of the original model and the absence of adequate connection with a fundamental mechanism of microbial spore inactivation based on the targeted blocking of the system of spore germination initialisation in combination with the conditions of the environment.

Consequently, there is no reason to believe that heat treatment regimes based on these empirical models were the most effective and provided a maximum sterilising effect at a minimum heat load. Thus, the analysis was the first link in arguing the necessity to initiate the research aimed at developing a methodology for determining the regimes of thermal sterilisation for food products including the analysis of the fundamental factors of spore germination activation and their resistance to external impact.

КОНФЛИКТ ИНТЕРЕСОВ

The authors state that there is no conflict of interest.

СПИСОК ЛИТЕРАТУРЫ

1. Galstyan AG, Radaeva IA, Chervetsov VV, Turovskaya SN, Illarionova EE, Petrov AN. Obnovlennye mezhgosudarstvennye standarty na konservy [Updated interstate standards for canned food]. Milk Processing. 2016;197(3):28–33. (In Russ.).
2. Prosekov AY, Ivanova SA. Food security: The challenge of the present. Geoforum. 2018;91:73–77. DOI: https://doi.org/10.1016/j.geoforum.2018.02.030.
3. Galstyan AG, Aksyonova LM, Lisitsyn AB, Oganesyants LA, Petrov AN. Modern approaches to storage and effective processing of agricultural products for obtaining high-quality food products. Vestnik Rossijskoj akademii nauk. 2019;89(5):539–542. (In Russ.). DOI: https://doi.org/10.31857/S0869-5873895539-542.
4. Turovskaya SN, Galstyan AG, Petrov AN, Radaeva IA, Illarionova EE, Semipyatniy VK, et al. Safety of canned milk as an integrated criterion of their technology effectiveness. Russian experience. Food Systems. 2018;1(2):29–54. (In Russ.). DOI: https://doi.org/10.21323/2618-9771-2018-1-2-29-54.
5. Barron UAG. Modeling Thermal Microbial Inactivation Kinetics. In: Sun D-W, editor. Thermal Food Processing: New Technologies and Quality Issues, Second Edition. CRC Press; 2012. pp. 151–191. DOI: https://doi.org/10.1201/b12112.
6. Bevilacqua A, Speranza B, Sinigaglia M, Corbo MR. A Focus on the Death Kinetics in Predictive Microbiology: Benefits and Limits of the Most Important Models and Some Tools Dealing with Their Application in Foods. Foods. 2015;4(4):565–580.
7. Forghani F, den Bakker M, Futral AN, Diez-Gonzalez F. Long-Term Survival and Thermal Death Kinetics of Enterohemorrhagic Escherichia coli Serogroups O26, O103, O111, and O157 in Wheat Flour. Applied and Environmental Microbiology. 2018;84(13). DOI: https://doi.org/10.1128/aem.00283-18.
8. Li R, Kou XX, Zhang LH, Wang SJ. Inactivation kinetics of food-borne pathogens subjected to thermal treatments: a review. International Journal of Hyperthermia. 2018;34(2):177–188. DOI: https://doi.org/10.1080/02656736.2017. 1372643.
9. Whiting RC, Buchanan RL. Predictive microbiology In: Doyle MP, Beuchat LR, Montville TJ, editors. Food Microbiology: Fundamentals and Frontier. Washington, DC: ASM Press; 1997. pp. 728–739.
10. Chick H. An Investigation of the Laws of Disinfection. Journal of Hygiene. 1908;8(1):92–158. DOI: https://doi.org/10.1017/S0022172400006987.
11. Bigelow WD, Bohart GS, Richardson AC, Ball CO. Heat Penetration in Processing Canned Foods. Washington, DC: Research Laboratory, National Canners Association; 1920.
12. Bigelow WD. The logarithmic nature of thermal death time curves. Journal of Infectious Diseases. 1921;29(5):528–536. DOI: https://doi.org/10.1093/infdis/29.5.528.
13. Schaffner DW, Labuza TP. Predictive microbiology: Where are we, and where are we going? Food Technology. 1997;51(4):95–99.
14. Peleg M, Engel R, Gonzalez-Martinez C, Corradini MG. Non-Arrhenius and non-WLF kinetics in food systems. Journal of the Science of Food and Agriculture. 2002;82(12):1346–1355. DOI: https://doi.org/10.1002/jsfa.1175.
15. Xiong R, Xie G, Edmondson AE, Sheard MA. A mathematical model for bacterial inactivation. International Journal of Food Microbiology. 1999;46(1):45–55. DOI: https://doi.org/10.1016/s0168-1605(98)00172-x.
16. McKellar RC, Lu X. Modelling microbial responses in foods. CRC Press, 2003. 360 p.
17. Buchanan RL, Golden MH, Whiting RC. Differentiation of the effects of pH and lactic or acetic-acid concentration on the kinetics of listeria-monocytogenes inactivation. Journal of Food Protection. 1993;56(6):474–478.
18. Whiting RC. Modeling bacterial survival in unfavorable environments. Journal of Industrial Microbiology. 1993;12 (3–5):240–246. DOI: https://doi.org/10.1007/bf01584196.
19. van Boekel M. On the use of the Weibull model to describe thermal inactivation of microbial vegetative cells. International Journal of Food Microbiology. 2002;74(1–2):139–159. DOI: https://doi.org/10.1016/s0168-1605(01)00742-5.
20. Mafart P, Couvert O, Gaillard S, Leguerinel I. On calculating sterility in thermal preservation methods: application of the Weibull frequency distribution model. International Journal of Food Microbiology. 2002;72(1–2):107–113. DOI: https://doi.org/10.1016/s0168-1605(01)00624-9.
21. Bhaduri S, Smith PW, Palumbo SA, Turner-Jones CO, Smith JL, Marmer BS, et al. Thermal destruction of Listeria monocytogenes in liver sausage slurry. Food Microbiology. 1991;8:75–78.
22. Casolari A. Microbial death. In: Bazin MJ, Prosser JL, editors. Physiological Models in Microbiology. Volume 2. Boca Raton, FL: CRC Press; 1988. pp. 1–44.
23. Geeraerd AH, Herremans CH, Van Impe JF. Structural model requirements to describe microbial inactivation during a mild heat treatment. International Journal of Food Microbiology. 2000;59(3):185–209. DOI: https://doi.org/10.1016/s0168-1605(00)00362-7.
24. Daugthry BJ, Davey KR, Thomas CJ, Verbyla AP. Food processing – a new model for the thermal destruction of contaminating bacteria. In: Jowitt R, editor. Engineering and Food at ICEF7. Sheffield: Sheffield Academic Press; 1997. pp. A113–A116.
25. McKellar RC, Lu X. Primary Models. In: McKellar RC, Lu X, editors. Modelling microbial responses in foods. CRC Press, 2003. pp. 21–27.
26. Bermudez-Aguirre D, Corradini MG. Inactivation kinetics of Salmonella spp. under thermal and emerging treatments: A review. Food Research International. 2012;45(2):700–712. DOI: https://doi.org/10.1016/j.foodres.2011.05.040.
27. Cole MB, Davies KW, Munro G, Holyoak CD, Kilsby DC. A vitalistic model to describe the thermal inactivation of listeria-monocytogenes. Journal of Industrial Microbiology. 1993;12(3–5):232–239. DOI: https://doi.org/10.1007/bf01584195.
28. Membre JM, Majchrzak V, Jolly I. Effects of temperature, pH, glucose, and citric acid on the inactivation of Salmonella typhimurium in reduced calorie mayonnaise. Journal of Food Protection. 1997;60(12):1497–1501.
29. Kamau DN, Doores S, Pruitt KM. Enhanced thermal-destruction of listeria-monocytogenes and Staphylococcusaureus by the lactoperoxidase system. Applied and Environmental Microbiology. 1990;56(9):2711–2716.
30. Xiong R, Xie G, Edmondson AS, Linton RH, Sheard MA. Comparison of the Baranyi model with the modified Gompertz equation for modelling thermal inactivation of Listeria monocytogenes Scott A. Food Microbiology. 1999;16(3):269–279. DOI: https://doi.org/10.1006/fmic.1998.0243.
31. Augustin JC, Carlier V, Rozier J. Mathematical modelling of the heat resistance of Listeria monocytogenes. Journal of Applied Microbiology. 1998;84(2):185–191.
32. Fernandez A, Salmeron C, Fernandez PS, Martinez A. Application of a frequency distribution model to describe the thermal inactivation of two strains of Bacillus cereus. Trends in Food Science & Technology. 1999;10(4–5):158–162. DOI: https://doi.org/10.1016/s0924-2244(99)00037-0.
33. Chiruta J, Davey KR, Thomas CJ. Combined effect of temperature and pH on microbial death in continuous pasteurization of liquids. In: Jowitt R, editor. Engineering and Food at ICEF7. Sheffield: Sheffield Academic Press; 1997. pp. A109–A112.
34. Cerf O. Tailing of survival curves of bacterial-spores. Journal of Applied Bacteriology. 1977;42(1):1–19. DOI: https://doi.org/10.1111/j.1365-2672.1977.tb00665.x.
35. Whiting RC, Buchanan RL. Use of predictive microbial modeling in a HACCP program. Proceedings of the Second ASEPT International Conference: Predictive Microbiology and HACCP; 1992; Laval. Laval: ASEPT; 1992. pp. 125–141.
36. Coroller L, Leguerinel I, Mettler E, Savy N, Mafart P. General Model, Based on Two Mixed Weibull Distributions of Bacterial Resistance, for Describing Various Shapes of Inactivation Curves. Applied and Environmental Microbiology. 2006;72(10):6493–6502. DOI: https://doi.org/10.1128/aem.00876-06.
37. Method on the Detection of Taint Producing Alicyclobacillus in Fruit Juices. 2007.
38. Aneja KR, Dhiman R, Kumar NA, Aneja A. Review Article. Emerging Preservation Techniques for Controlling Spoilage and Pathogenic Microorganisms in Fruit Juices. International Journal of Microbiology. 2014;2014. DOI: https://doi.org/10.1155/2014/758942.
39. ISO 7218:2007. Microbiology of Food and Animal Feeding Stuffs – General Requirements and Guidance for Microbiological Examinations. 2013.